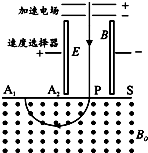
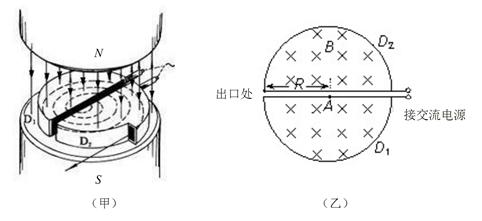
题目内容
在图示区域中,x轴上方有一匀强磁场,磁感应强度大小为B,方向垂直纸面向里,x轴下方有一匀强电场.现有一质子以速度v0由y轴上的A点沿y轴正方向射入磁场,质子在磁场中运动一段时间后从C点与x轴成45°角进入匀强电场区域,经时间t原路返回再次进入磁场继续运动.己知质子质量为m,电最为q,不计重力,磁场区域和电场区域足够大.求:
(1)C点的x坐标;
(2)匀强电场的场强大小和方向;
(3)质子第四次穿过x轴时的x坐标.

(1)C点的x坐标;
(2)匀强电场的场强大小和方向;
(3)质子第四次穿过x轴时的x坐标.

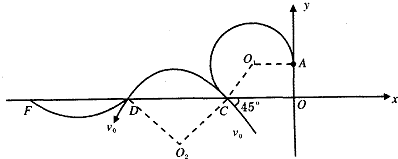
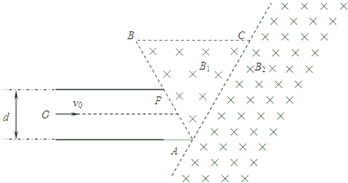
质子的运动轨迹如图
(1)质子的轨迹半径为R=
C点的坐标为xc=-R(1+
)=-
(1+
)
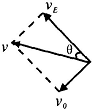
(2)粒子在电场中做直线运动,并且经时间t原路返回再次进入磁场,根据运动的对称性可知,返回磁场时的速度与出磁场时的速度大小相等,方向相反;
所以电场的方向必定与x轴负方向成45°角,斜向上.
根据动量定理可得-qEt=-mv0-mv0
所以:E=
(3)质子第二次穿越χ轴后,在磁场中作圆周运动,运动的半径与第一次时相同,轨迹如图,
由于粒子的轨迹是
圆弧,所以:
=2R=
质子第三次穿越χ轴后,在电场中作类平抛运动,由于V0与χ负方向成45°角,所以第四次穿越x轴时沿v0方向的位移与垂直于v0方向的位移大小相等,即:
v0t′=
?
?t′2
解得,t′=t.
所以:
=
v0t′=
v0t
代人数据得:
=
(1+
)+
+
v0t=
(3+
)+
v0t
故F点的坐标为:([-
(3+
)+
v0t],0)
答:(1)C点的坐标是 [-
(1+
),0].
(2)匀强电场的场强大小E=
,方向与x轴负方向成45°角,斜向上.
(3)质子第四次穿越χ轴时的坐标为:([-
(3+
)+
v0t],0)
(1)质子的轨迹半径为R=
| mv0 |
| qB |
C点的坐标为xc=-R(1+
| ||
| 2 |
| mv0 |
| qB |
| ||
| 2 |
(2)粒子在电场中做直线运动,并且经时间t原路返回再次进入磁场,根据运动的对称性可知,返回磁场时的速度与出磁场时的速度大小相等,方向相反;
所以电场的方向必定与x轴负方向成45°角,斜向上.
根据动量定理可得-qEt=-mv0-mv0
所以:E=
| 2mv0 |
| qt |
(3)质子第二次穿越χ轴后,在磁场中作圆周运动,运动的半径与第一次时相同,轨迹如图,
由于粒子的轨迹是
| 1 |
| 4 |
| . |
| CD |
| 2mv0 |
| qB |
质子第三次穿越χ轴后,在电场中作类平抛运动,由于V0与χ负方向成45°角,所以第四次穿越x轴时沿v0方向的位移与垂直于v0方向的位移大小相等,即:
v0t′=
| 1 |
| 2 |
| qE |
| m |
解得,t′=t.
所以:
| . |
| DF |
| 2 |
| 2 |
代人数据得:
| . |
| OF |
| mv0 |
| qB |
| ||
| 2 |
| 2mv0 |
| qB |
| 2 |
| mv0 |
| qB |
| ||
| 2 |
| 2 |
故F点的坐标为:([-
| mv0 |
| qB |
| ||
| 2 |
| 2 |
答:(1)C点的坐标是 [-
| mv0 |
| qB |
| ||
| 2 |
(2)匀强电场的场强大小E=
| 2mv0 |
| qt |
(3)质子第四次穿越χ轴时的坐标为:([-
| mv0 |
| qB |
| ||
| 2 |
| 2 |



练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目

 q=-1.0×10-4C;带电粒子恰好从P点垂直AB边以速度v=2×105m/s进入磁场,则
q=-1.0×10-4C;带电粒子恰好从P点垂直AB边以速度v=2×105m/s进入磁场,则