��Ŀ����
����Ŀ����ֱƽ���ڵİ�Բ����⻬����ˮƽ����������B�㣬һ����Ϊ1kg�ļ�ӲС���A������Ϊ�ʵ㣩����ֹ�ڹ⻬��ˮƽ�����ϣ���ͼ��ʾ��һ������Ϊ10g���ӵ���505m/s���ٶ�������������ô��в�����С����ڣ�����һ�������˶�����֪R=0.4m��g=10m/s2 �� ��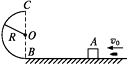
���ӵ�����С��鲢�ϳ�һ������ʱ�Ĺ�ͬ�ٶȣ�
��С�����C��Թ�����˵�ѹ����С��
��С�����ص���B���ˮƽ���룮
���𰸡��⣺���ӵ�����С���Ĺ��̣�ȡ����Ϊ�������ɶ����غ㶨�ɵã�
mv0=��m+M��v
�ù�ͬ����ٶ�Ϊ��v= ![]() =
= ![]() =5m/s
=5m/s
��С��飨���ӵ�����A�˶���C��Ĺ��̣��ɻ�е���غ㶨�ɵã�
![]() =
= ![]() +��m+M��g2R
+��m+M��g2R
�������ݽ�ã�vC=3m/s
��C�㣬��ţ�ٵڶ����ɵã�
N+��m+M��g=��m+M�� ![]()
�������ݽ�� N=12.625N
��ţ�ٵ�������֪��С�����C��Թ�����˵�ѹ����СΪ��N��=N=12.625N��
��С����뿪C�����ƽ���˶������У�
2R= ![]()
x=vCt
���С�����ص���B���ˮƽ����Ϊ��x=1.2m
�𣺢��ӵ�����С��鲢�ϳ�һ������ʱ�Ĺ�ͬ�ٶ���5m/s��
��С�����C��Թ�����˵�ѹ����С��12.625N��
��С�����ص���B���ˮƽ������1.2m��
�����������ӵ����С���Ĺ������ض����غ㣬�ɶ����غ㶨�������߲��ϳ�һ������ʱ�Ĺ�ͬ�ٶȣ�������û��Ħ�������Թ�ͬ���A�˶���C�Ĺ����У���е���غ㣬�ɻ�е���غ㶨�������ͬ�嵽��C��ʱ���ٶȣ�����ţ���˶��������С�����C��Թ�����˵�ѹ����С����С����뿪C�����ƽ���˶����ɷ�λ�ƹ�ʽ����ص���B���ˮƽ���룮
�����㾫��������ƽ���˶��Ͷ����غ㶨�ɶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶��������غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮

 ��У����ϵ�д�
��У����ϵ�д�