��Ŀ����
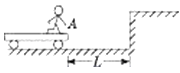
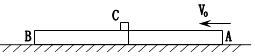
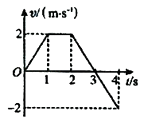
����Ŀ����ͼ��ʾ��ˮƽ�����Ͼ�ֹ����һ��С��A������mA=4kg���ϱ���⻬��С���������Ħ������С�����Ժ��Բ��ƣ�����Ϊ�ʵ�����B����A�����Ҷˣ�B������mB=2kg���ֶ�Aʩ��һ��ˮƽ���ҵĺ���F=10N��A�˶�һ��ʱ���С����˹̶��ĵ�����B������ײ����ײʱ�伫�̣�����A��Bճ����һ�𣬹�ͬ��F�������¼����˶�����ײ��ʱ��t=0.6s�����ߵ��ٶȴﵽvt=2m/s����
��1��A��ʼ�˶�ʱ���ٶ�a�Ĵ�С��
��2��A��B��ײ��˲��Ĺ�ͬ�ٶ�v�Ĵ�С��
��3��A���ϱ��泤��l��
���𰸡�
��1���⣺��AΪ�о�������ţ�ٵڶ����ɵã�
F=mAa��
�������ݵã�a=2.5m/s2��
��A��ʼ�˶�ʱ���ٶ�a�Ĵ�СΪ2.5m/s2��
��2��A��B��ײ��ͬ�˶������У�ѡ���ҵķ���Ϊ�����ɶ��������ã�
Ft=��mA+mB��vt����mA+mB��v��
�������ݽ�ã�v=1m/s��
��A��B��ײ��˲��Ĺ�ͬ�ٶ�v�Ĵ�СΪ1m/s��
��3��A��B��ײ���̶����غ㣬��A�ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�
mAvA=��mA+mB��v��
A�ӿ�ʼ�˶�����B������ײǰ���ɶ��ܶ����ã�
Fl= ![]() mAvA2��0��
mAvA2��0��
�������������ݵã�l=0.45m��
��A���ϱ��泤��Ϊ0.45m��
����������1������ţ�ٵڶ��˶�����ֱ����ʽ������ٶȡ�
��2���������ж�������ʽ�ӣ�����ٶ�ĩ��ע�����ǰ��ѡ��������
��3����ײ���̣����㶯���غ�������غ㣬���ݶ����غ�Ͷ��ܶ�������ʽ��⡣
�����㾫����������Ĺؼ���������ܶ������ۺ�Ӧ�õ����֪ʶ������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ��Լ��Զ������������⣬�˽���������о���������ǵ������壬Ҳ����������ϵͳ.������ϵͳ��ֻ�����ϵͳ�ܵ����������ؿ���ϵͳ����.ϵͳ���������ò��ı�����ϵͳ���ܶ����������������������ں㶨������Ҳ��������ʱ��仯����.���ڱ��������������е���FӦ������Ϊ����������ʱ���ڵ�ƽ��ֵ��

 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�