题目内容
17.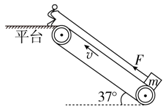 如图所示,一传送带与水平地面的夹角θ=37°,传送带上端固定一平台,平台离地面高H=1.8m,传送带以恒定速度v=4m/s逆时针运行.将质量m=2kg的小滑块轻放在传送带底端,平台上的人通过一根轻绳用恒力F沿传送带向上拉小滑块,滑块的速度刚达到传送带的速度时轻绳断裂,此后小滑块恰好不能到平台上,已知滑块与传送带之间的动摩擦因数μ=0.25,最大静摩擦力等于滑动摩擦力,g取10m/s2.已知sin37°=0.6,cos37°=0.8,求:
如图所示,一传送带与水平地面的夹角θ=37°,传送带上端固定一平台,平台离地面高H=1.8m,传送带以恒定速度v=4m/s逆时针运行.将质量m=2kg的小滑块轻放在传送带底端,平台上的人通过一根轻绳用恒力F沿传送带向上拉小滑块,滑块的速度刚达到传送带的速度时轻绳断裂,此后小滑块恰好不能到平台上,已知滑块与传送带之间的动摩擦因数μ=0.25,最大静摩擦力等于滑动摩擦力,g取10m/s2.已知sin37°=0.6,cos37°=0.8,求:(1)恒力F?
(2)小滑块在传送带上运动的总时间T?
分析 (1)绳子断裂后,滑块做匀减速运动,根据牛顿第二定律求出加速度,结合速度位移公式求出匀减速运动的位移,从而得出匀加速运动的位移,根据速度位移公式求出匀加速运动的加速度,结合牛顿第二定律求出恒力F的大小
(2)滑块先向上做匀加速直线运动,然后做匀减速运动到零,再返回做匀加速直线运动,结合运动学公式求出各段的时间,从而得出总时间.
解答 解:(1)绳子断裂后,滑块做匀减速运动,加速度大小${a}_{2}=\frac{mgsin37°-μmgcos37°}{m}$=gsin37°-μgcos37°=6-0.25×8=4m/s2.
因为滑块恰好不能到达平台,则匀减速运动的位移${x}_{2}=\frac{{v}^{2}}{2{a}_{2}}=\frac{16}{8}=2m$,
可知匀加速运动的位移${x}_{1}=\frac{H}{sin37°}-{x}_{2}=\frac{1.8}{0.6}-2m=1m$,
匀加速运动的加速度${a}_{1}=\frac{{v}^{2}}{2{x}_{1}}=\frac{16}{2}=8m/{s}^{2}$,
根据牛顿第二定律得,F-mgsin37°+μmgcos37°=ma1,
代入数据解得F=24N.
(2)匀加速运动的时间${t}_{1}=\frac{v}{{a}_{1}}=\frac{4}{8}s=0.5s$,
匀减速运动的时间${t}_{2}=\frac{v}{{a}_{2}}=\frac{4}{4}s=1s$,
返回做匀加速运动的加速度${a}_{3}=\frac{mgsin37°-μmgcos37°}{m}$=gsin37°-μgcos37°=6-0.25×8=4m/s2.
根据$\frac{H}{sin37°}=\frac{1}{2}{a}_{3}{{t}_{3}}^{2}$得,${t}_{3}=\sqrt{\frac{2×\frac{1.8}{0.6}}{4}}s≈1.2s$,
则小滑块在传送带上运动的总时间T=t1+t2+t3=0.5+1+1.2s=2.7s.
答:(1)恒力F为24N.
(2)小滑块在传送带上运动的总时间T为2.7s.
点评 解决本题的关键理清滑块在传送带上的运动规律,结合牛顿第二定律和运动学公式综合求解,知道加速度是联系力学和运动学的桥梁.

 A、B为两个固定的等量同种正点电荷,O为AB连线的中点,另一个也带正电的重力不计的小电荷静止于O点,如图所示,则( )
A、B为两个固定的等量同种正点电荷,O为AB连线的中点,另一个也带正电的重力不计的小电荷静止于O点,如图所示,则( )| A. | 使小电荷向右偏离一点,释放后将向左先加速后减速直至停到某一位置 | |
| B. | 使小电荷向左偏离一点,释放后将做以O点为中心的往复运动 | |
| C. | 使小电荷向上方偏离一点,释放后将做以O点为中心的往复运动 | |
| D. | 使小电荷向下方偏离一点,释放后将向下做加速度先变大后变小的变加速运动 |
| 制动时速度/(km•h-1) | 反应距离/m | 制动距离/m | 停车总距离/m |
| 40 | 8 | ||
| 120 |
| A. | 电场强度为零的区域内,电势也一定为零 | |
| B. | 电场强度的方向总是跟等势面垂直 | |
| C. | 电场强度处处相同的区域内,电势也一定处处相同 | |
| D. | 沿着电场强度的方向,电势总是不断降低的 |
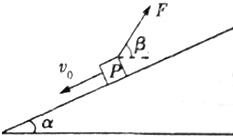 如图所示,斜面倾角为α=37°,在斜面上有一质量为m=1kg的物体P正在沿斜面向下滑动,P与斜面间的动摩擦因数为μ=0.5,当物体P的速度为v0=6m/s时受到一个与水平面成夹角β=74°斜向上的拉力F=10N的作用,拉力作用时间t1=6s,sin37°=0.6,cos37°=0.8,g=10m/s2,求:
如图所示,斜面倾角为α=37°,在斜面上有一质量为m=1kg的物体P正在沿斜面向下滑动,P与斜面间的动摩擦因数为μ=0.5,当物体P的速度为v0=6m/s时受到一个与水平面成夹角β=74°斜向上的拉力F=10N的作用,拉力作用时间t1=6s,sin37°=0.6,cos37°=0.8,g=10m/s2,求: 如图所示,在坐标系的第一象限内有匀强电场,其场强为E0,一个质量为m,电量为q的正电荷从A点以初速度为v0沿x轴正方向运动,正好到达x轴上的B点,在第四第象限内有垂直于纸面向外的匀强磁场,当电荷到达C点时速度恰好平行于x轴,电荷由C点进入第三象限,然后由D点进入第二象限,已知OA=d,OB=2d,OD=2d,求.
如图所示,在坐标系的第一象限内有匀强电场,其场强为E0,一个质量为m,电量为q的正电荷从A点以初速度为v0沿x轴正方向运动,正好到达x轴上的B点,在第四第象限内有垂直于纸面向外的匀强磁场,当电荷到达C点时速度恰好平行于x轴,电荷由C点进入第三象限,然后由D点进入第二象限,已知OA=d,OB=2d,OD=2d,求.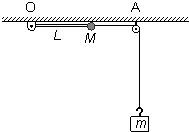 如图所示,天花板上有固定转轴O,长为L的轻杆一端可绕转轴O在竖直平面内自由转动,另一端固定一质量为M的小球.一根不可伸长的足够长轻绳绕过定滑轮A,一端与小球相连,另一端挂着质量为m1的钩码,定滑轮A的位置可以沿OA连线方向调整.小球、钩码均可看作质点,不计一切摩擦,g取10m/s2.
如图所示,天花板上有固定转轴O,长为L的轻杆一端可绕转轴O在竖直平面内自由转动,另一端固定一质量为M的小球.一根不可伸长的足够长轻绳绕过定滑轮A,一端与小球相连,另一端挂着质量为m1的钩码,定滑轮A的位置可以沿OA连线方向调整.小球、钩码均可看作质点,不计一切摩擦,g取10m/s2.