��Ŀ����
2�� ��ͼ��ʾ��������ϵ�ĵ�һ����������ǿ�糡���䳡ǿΪE0��һ������Ϊm������Ϊq������ɴ�A���Գ��ٶ�Ϊv0��x���������˶������õ���x���ϵ�B�㣬�ڵ��ĵ��������д�ֱ��ֽ���������ǿ�ų�������ɵ���C��ʱ�ٶ�ǡ��ƽ����x�ᣬ�����C�����������ޣ�Ȼ����D�����ڶ����ޣ���֪OA=d��OB=2d��OD=2d����
��ͼ��ʾ��������ϵ�ĵ�һ����������ǿ�糡���䳡ǿΪE0��һ������Ϊm������Ϊq������ɴ�A���Գ��ٶ�Ϊv0��x���������˶������õ���x���ϵ�B�㣬�ڵ��ĵ��������д�ֱ��ֽ���������ǿ�ų�������ɵ���C��ʱ�ٶ�ǡ��ƽ����x�ᣬ�����C�����������ޣ�Ȼ����D�����ڶ����ޣ���֪OA=d��OB=2d��OD=2d������1��������������ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�С��
��2��������������ǿ�ų��ij�ǿE���һ������E0֮�ȣ�
��3����ɵ���D��ʱ�Ķ���Ek���
���� ��1�������ڵ�һ����������ƽ���˶�����ƽ���˶���֪ʶ������ӽ�����������ٶȵĴ�С�ͷ����������ڴų����˶��Ĺ켣��Ȼ���ɼ��ι�ϵ��������˶��İ뾶���ɰ뾶��ʽ����Ÿ�Ӧǿ�ȣ�
��2�������ڵ�������������ƽ���˶�������˶��ĺϳ���ֽ��֪ʶ��������糡ǿ�ȣ�
��3�������ڵ�������������ƽ���˶�������˶��ĺϳ���ֽ��֪ʶ������ӵ���D����ٶȣ��ɶ��ܵĶ���ʽ���������ɵ���D��ʱ�Ķ��ܣ�
��� �⣺��1�������ڵ�һ����������ƽ���˶���ˮƽ����2d=v0t
��ֱ�������ȼ���ֱ���˶������ԣ�$d=\frac{{v}_{y}}{2}•t$
�����ɵã�vy=v0
���ӵ��ٶȷ�����ˮƽ����֮��ļнǦȣ�tan��=$\frac{{v}_{y}}{{v}_{0}}=\frac{{v}_{0}}{{v}_{0}}=1$
���ԣ���=45��
���ӽ���ų����ٶȣ�v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}=\sqrt{2}{v}_{0}$
�������ڴ�ֱ��y�����������ޣ����Ի����˶��Ĺ켣��ͼ��
��ͼ��֪�������ڴų����˶��İ뾶��$r=\sqrt{2}OB=2\sqrt{2}d$
�����ڴų����ܵ�����������ͨ������������$\frac{m{v}^{2}}{r}=qvB$
�����ã�B=$\frac{m{v}_{0}}{2qd}$
��2�������ڵ����������˶���ʱ��t�䣬��2d=vt��
���ԣ�$t��=\frac{\sqrt{2}}{2}t$
O��C��ľ��룺L=$OP+PC=OB+r=��2+2\sqrt{2}��d$
��ֱ����L=$\frac{1}{2}•\frac{qE}{m}•t{��}^{2}$
�ڵ�һ���ޣ�$d=\frac{1}{2}•\frac{q{E}_{0}}{m}•{t}^{2}$
�����ã�$E=��4+4\sqrt{2}��{E}_{0}$
��3�����ӵ���D������ֱ����ķ��ٶ���vy�䣬��$L=\frac{{v}_{y}��}{2}•t��$
���ӵ���D����ٶȣ�${v}_{D}=\sqrt{{v}^{2}+v{��}_{y}^{2}}$
���ӵĶ��ܣ�${E}_{K}=\frac{1}{2}m{v}_{D}^{2}$
�����ã�${E}_{k}=��11+8\sqrt{2}��m{v}_{0}^{2}$
�𣺣�1��������������ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�С��$\frac{m{v}_{0}}{2qd}$��
��2��������������ǿ�ų��ij�ǿE���һ������E0֮����$4+4\sqrt{2}$��
��3����ɵ���D��ʱ�Ķ���Ek��$��11+8\sqrt{2}��m{v}_{0}^{2}$��
���� ������Ҫ�����˴��������ڻ�ϳ����˶������⣬Ҫ��ͬѧ������ȷ�������ӵ������������ͨ����������������ӵ��˶��������������Բ���˶���ƽ���˶��Ļ�����ʽ���Ѷ����У�

 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ����ΪM�����ó�ΪL�����߹̶���O�㣬��O�����·�$\frac{L}{2}$����һ�Ŷ��ӣ���������ֱ����ֱ�����һ���Ƕȣ��ɾ�ֹ�ͷ�С����ͼ��ʾ����������������ʱ������˵����ȷ���ǣ�������
����ΪM�����ó�ΪL�����߹̶���O�㣬��O�����·�$\frac{L}{2}$����һ�Ŷ��ӣ���������ֱ����ֱ�����һ���Ƕȣ��ɾ�ֹ�ͷ�С����ͼ��ʾ����������������ʱ������˵����ȷ���ǣ�������| A�� | С��Ļ�е��ͻȻ���� | B�� | С������ļ��ٶ�ͻȻ���� | ||
| C�� | С��Ľ��ٶ�ͻȻ��С | D�� | ���ߵ�����ͻȻ���� |
 ��ͼ��ʾ��A��B��CΪ�糡��ͬһ�糡���ϵ����㣬��C��ΪAB���е㣮�����ڵ糡��ֻ�ܾ��������ã�����C�����ٵ��ͷ�һ������ɣ����������B�˶��������ܼ����ˡ�Ep������C�����ٵ��ͷŵ����ĸ���ɣ������A�˶��������ܼ����ˡ�Ep�䣮�������ж���ȷ���ǣ�������
��ͼ��ʾ��A��B��CΪ�糡��ͬһ�糡���ϵ����㣬��C��ΪAB���е㣮�����ڵ糡��ֻ�ܾ��������ã�����C�����ٵ��ͷ�һ������ɣ����������B�˶��������ܼ����ˡ�Ep������C�����ٵ��ͷŵ����ĸ���ɣ������A�˶��������ܼ����ˡ�Ep�䣮�������ж���ȷ���ǣ�������| A�� | ��Ep=��Ep�� | B�� | ��Ep����Ep�� | C�� | ��Ep����Ep�� | D�� | ���ж� |
 ��ͼ��ʾ����Ϊ16N�����G1������ϸ�������´��ھ�ֹ״̬��ϸ��BP��ˮƽ����ϸ��APƫ����ֱ����37��ǣ���������Ϊ50N�����G2�ϣ����G2��ֹ�����Ϊ37���б���� ��sin37��=0.6��cos37��=0.8����ȡg=10m/s2��������˵����ȷ���ǣ�������
��ͼ��ʾ����Ϊ16N�����G1������ϸ�������´��ھ�ֹ״̬��ϸ��BP��ˮƽ����ϸ��APƫ����ֱ����37��ǣ���������Ϊ50N�����G2�ϣ����G2��ֹ�����Ϊ37���б���� ��sin37��=0.6��cos37��=0.8����ȡg=10m/s2��������˵����ȷ���ǣ�������| A�� | ��PB�����G2������9 N | B�� | ��PA��P�������20N | ||
| C�� | б������G2��Ħ����32.8 N | D�� | б������G2��֧����39.6 N |
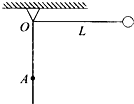 ��ͼ��ʾ����ΪL��ϸ��һ�˹̶���O�㣬��һ��˩סһ��С����O������·���O�����$\frac{2L}{3}$�ĵط���һö����ֱƽ�洹ֱ�Ķ���A����������ʹϸ����ˮƽ������ֱ���ɾ�ֹ��ʼ�ͷţ���ϸ���������Ӻ��˲�䣨ϸ��û�жϣ�������˵������ȷ���ǣ�������
��ͼ��ʾ����ΪL��ϸ��һ�˹̶���O�㣬��һ��˩סһ��С����O������·���O�����$\frac{2L}{3}$�ĵط���һö����ֱƽ�洹ֱ�Ķ���A����������ʹϸ����ˮƽ������ֱ���ɾ�ֹ��ʼ�ͷţ���ϸ���������Ӻ��˲�䣨ϸ��û�жϣ�������˵������ȷ���ǣ�������| A�� | С��Ľ��ٶ�ͻȻ����ԭ����1.5�� | |
| B�� | С������ٶ�ͻȻ����ԭ����3�� | |
| C�� | С������ļ��ٶ�ͻȻ����ԭ����3�� | |
| D�� | ϸ����С�������ͻȻ����ԭ����1.5�� |
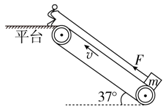 ��ͼ��ʾ��һ���ʹ���ˮƽ����ļнǦ�=37�㣬���ʹ��϶˹̶�һƽ̨��ƽ̨������H=1.8m�����ʹ��Ժ㶨�ٶ�v=4m/s��ʱ�����У�������m=2kg��С��������ڴ��ʹ��ˣ�ƽ̨�ϵ���ͨ��һ�������ú���F�ش��ʹ�������С���飬������ٶȸմﵽ���ʹ����ٶ�ʱ�������ѣ��˺�С����ǡ�ò��ܵ�ƽ̨�ϣ���֪�����봫�ʹ�֮��Ķ�Ħ��������=0.25�����Ħ�������ڻ���Ħ������gȡ10m/s2����֪sin37��=0.6��cos37��=0.8����
��ͼ��ʾ��һ���ʹ���ˮƽ����ļнǦ�=37�㣬���ʹ��϶˹̶�һƽ̨��ƽ̨������H=1.8m�����ʹ��Ժ㶨�ٶ�v=4m/s��ʱ�����У�������m=2kg��С��������ڴ��ʹ��ˣ�ƽ̨�ϵ���ͨ��һ�������ú���F�ش��ʹ�������С���飬������ٶȸմﵽ���ʹ����ٶ�ʱ�������ѣ��˺�С����ǡ�ò��ܵ�ƽ̨�ϣ���֪�����봫�ʹ�֮��Ķ�Ħ��������=0.25�����Ħ�������ڻ���Ħ������gȡ10m/s2����֪sin37��=0.6��cos37��=0.8����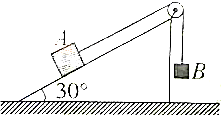 ��ͼ��ʾ��б����̶���ˮƽ�����ϣ�б���嶥����һ�Ử�֣�������ֵ���ϸ��һ������ڹ⻬б���ϵ����A��������һ�������B��������֪���A������Ϊm�����B������Ϊ2m����ʼʱ���B�����ĸ߶�Ϊh���������ٶ�Ϊg��б���㹻�����ְ����A�ɾ�ֹ�ͷţ���
��ͼ��ʾ��б����̶���ˮƽ�����ϣ�б���嶥����һ�Ử�֣�������ֵ���ϸ��һ������ڹ⻬б���ϵ����A��������һ�������B��������֪���A������Ϊm�����B������Ϊ2m����ʼʱ���B�����ĸ߶�Ϊh���������ٶ�Ϊg��б���㹻�����ְ����A�ɾ�ֹ�ͷţ���