题目内容
【题目】如图所示，一倾斜固定的传送带（足够长）与水平面的倾角
，传送带以v=2m/s的速率沿顺时针方向勾速运行。从传送带上到传送带底端距离x0=4m的O点由静止释放一质量m=0.5kg的滑块（视为质点），滑块由静止释放后沿传送带向下运动，到达传送带底端时与挡板P发生碰撞，滑块与挡板P碰撞前后的速率不变。滑块与传送带间的动摩擦因数μ=
，取g=10 m/s2
(1)若滑块与挡板P第一次碰撞的时间t=0.02s，求该次碰撞过程中滑块所受合力大小的平均值F；
(2)求滑块与挡板P第一次碰撞后。到达的最高位置到传送带底端的距离L；
(3)求滑块以大于v的速率沿传送带上滑的总路程x。
【答案】(1)F=200N；(2) 
；(3)1m
【解析】
（1）滑块由静止释放后，沿传送带向下匀加速运动至传送带的底端，该过程中滑块的加速度大小为
滑块到达传送带底端时的速率为
由动量定理有
Ft=2mv1
解得F=200N
（2）滑块与挡板P第一次碰撞后，先沿传送带向上做匀减速运动至速率为v，该过程中滑块的加速度大小
该过程中滑块运动的距离为
此后，滑块以加速度a1继续沿传送带向上做匀减速运动至速率为零（此时滑块到达最高位置），该过程中滑块运动的距离为
故
（3）滑块与挡板P第一次碰撞到达最高位置后，沿传送带以加速度a1向下做匀加速运动到达传送带底端，与挡板P第二次碰撞，磁撞前瞬间的速率为
滑块与挡板P第二次碰撞后，先沿传送带向上以加速度a2做匀减速运动至速率为v，该过程中滑块运动的距离为
此后，滑块以加速度a1继续沿传送带向上做匀减速运动至速率为零，同理可得，该过程中滑块运动的距离为s2=s1=1m
滑块上升到最高位置后，沿传送带以加速度a1向下做匀加速运动到达传送带底端，与挡板P发生第三次碰撞，碰撞前瞬间的速率为
此后，滑块以加速度a1继续沿传送带向上做匀减速运动至速度为零，同理可得，该过程中滑块运动的距离为s3=1m
以此类推，经足够长时间，滑块与挡板P多次碰撞后，滑块以速率v反弹，此后，滑块在距传送带底端lm的范围往复运动
滑块每一次与挡板P碰撞后，沿传送带向上减速运动至速度为v的距离与滑块上一次与挡板P碰撞后沿传送带向上减速运动至速度为v的距离的比值均为
，根据数学知识可得
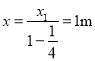
[或：(3)经分析可知，经足够长时间，滑块与挡板P多次碰撞后，最终将以速率v反弹，此后滑块在距传送带底端某恒定范围内往复运动
由动能定理可知，在滑块从第一次反弹后瞬间至到达传送带底端最终的速率第一次为v的过程中，摩擦力做的总功为
在滑块从第一次反弹后瞬间至到达传送带底端的速率第一次为v的过程中，滑块每次反弹后均先沿传送带向上以加速度a2做匀减速运动至速率为v（过程1）；再以加速度a1沿传送带向上做匀减速运动至速度为零，然后沿传送带向下以加速度a1做匀加速运动至速率为v（过程2）；最后沿传送带向下以加速度a1做匀加速运动至传送带的底端（过程3），根据对称性，在过程1与过程3中滑块运动的距离相等
因在过程2中摩擦力对滑块做的功为零，故整个过程中，摩擦力做的总功为
解得x=1m。
