题目内容
14. 如图,一位网球运动员用拍朝水平方向击球,第一只球落在自己一方场地上后弹跳起来刚好擦网而过,落在对方场地A处.第二只球直接擦网而过,也落在A处.球与地面的碰撞是完全弹性的,且空气阻力不计.
如图,一位网球运动员用拍朝水平方向击球,第一只球落在自己一方场地上后弹跳起来刚好擦网而过,落在对方场地A处.第二只球直接擦网而过,也落在A处.球与地面的碰撞是完全弹性的,且空气阻力不计.求(1)两次击球使球获得的水平初速度大小之比
(2)若网高h,击球高度为H,求$\frac{h}{H}$=?
分析 第一、二两球被击出后都是作平抛运动,竖直方向做自由落体运动,由于高度相同,两球被击出至各自第一次落地的时间是相等的.对于第一个球:球与地面的碰撞是完全弹性碰撞,撞地后弹起做斜抛运动,最大高度等于H,斜抛运动的时间等于被击出至各自第一次落地的时间的两倍.根据水平方向是匀速直线运动,研究出两个球的初速度关系,根据水平位移关系,研究初速度关系.再研究竖直方向的运动,化简求解$\frac{h}{H}$.
解答 解:(1)由平抛运动的规律可知,两球分别被击出至各自第一次落地的时间是相等的.由于球与地面的碰撞是完全弹性碰撞,设第一球自击出到落地时间为t1,第二球自击出到落地时间为t2,则:t1=3t2 ①
由于一、二两球在水平方向均为匀速运动,水平位移大小相等,设它们从O点出发时的初速度分别为v1、v2,由x=v0t得:
v2=3v1 ②
所以有$\frac{{v}_{1}}{{v}_{2}}=\frac{1}{3}$.
(2)设一、二两球从O点到C点时间分别为T1、T2,由于两球从O点到C点水平距离相等,则:
T1=3T2 ③
由竖直方向运动规律可知:
H=$\frac{1}{2}g(2{T}_{2})^{2}$ ④
h=$\frac{1}{2}g(2{T}_{2})^{2}-\frac{1}{2}g{{T}_{2}}^{2}$⑤
故得:$\frac{h}{H}=\frac{3}{4}$.
答:(1)两次击球使球获得的水平初速度大小之比为1:3;
(2)$\frac{h}{H}=\frac{3}{4}$.
点评 本题是较为复杂的平抛运动问题,考查解决复杂物理问题的能力.对于斜抛运动,可以等效看成两个平抛运动组成的

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
5.做离心运动的物体,下面说法正确的是( )
| A. | 离心现象是因为向心力小于离心力 | |
| B. | 离心现象是因为合外力不足以提供物体做圆周运动所需向心力 | |
| C. | 速度的大小改变,方向不变 | |
| D. | 速度大小和方向都可能改变 |
9.近期我国多个城市的PM2.5数值突破警戒线,受影响最严重的是京津冀地区,雾霾笼罩,大气污染严重.PM2.5是指空气中直径等于或小于2.5微米的悬浮颗粒物,其漂浮在空中做无规则运动,很难自然沉降到地面,吸入后对人体形成危害.矿物燃料燃烧的排放是形成PM2.5的主要原因.下列关于PM2.5的说法中正确的是( )
| A. | PM2.5的尺寸与空气中氧分子的尺寸的数量级相当 | |
| B. | PM2.5在空气中的运动属于布朗运动 | |
| C. | 温度越低PM2.5活动越剧烈 | |
| D. | 倡导低碳生活减步煤和石油等燃料的使用能有效减小PM2.5在空气中的浓度 | |
| E. | PM2.5中颗粒小一些的,其颗粒的运动比其它颗粒更为剧烈. |
19. 如图所示,沿直线通过速度选择器的正离子从狭缝S射入磁感应强度为B2的匀强磁场中,偏转后出现的轨迹半径之比为R1:R2=1:2,则下列说法正确的是( )
如图所示,沿直线通过速度选择器的正离子从狭缝S射入磁感应强度为B2的匀强磁场中,偏转后出现的轨迹半径之比为R1:R2=1:2,则下列说法正确的是( )
 如图所示,沿直线通过速度选择器的正离子从狭缝S射入磁感应强度为B2的匀强磁场中,偏转后出现的轨迹半径之比为R1:R2=1:2,则下列说法正确的是( )
如图所示,沿直线通过速度选择器的正离子从狭缝S射入磁感应强度为B2的匀强磁场中,偏转后出现的轨迹半径之比为R1:R2=1:2,则下列说法正确的是( )| A. | 离子的速度之比为1:1 | B. | 离子的电荷量之比为1:2 | ||
| C. | 离子的质量之比为1:2 | D. | 离子的荷质比为2:1 |
3.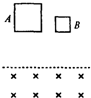 如图所示,A、B为不同金属制成的质量相等的正方形线框,A的边长是B的2倍,A的电阻是B的4倍,当它们的下边在同一高度竖直下落,垂直进入如图所示的磁场中,A框恰能匀速下落,那么( )
如图所示,A、B为不同金属制成的质量相等的正方形线框,A的边长是B的2倍,A的电阻是B的4倍,当它们的下边在同一高度竖直下落,垂直进入如图所示的磁场中,A框恰能匀速下落,那么( )
 如图所示,A、B为不同金属制成的质量相等的正方形线框,A的边长是B的2倍,A的电阻是B的4倍,当它们的下边在同一高度竖直下落,垂直进入如图所示的磁场中,A框恰能匀速下落,那么( )
如图所示,A、B为不同金属制成的质量相等的正方形线框,A的边长是B的2倍,A的电阻是B的4倍,当它们的下边在同一高度竖直下落,垂直进入如图所示的磁场中,A框恰能匀速下落,那么( )| A. | B框一定匀速下落 | |
| B. | 进入磁场后,A、B中感应电流强度之比是2:1 | |
| C. | 两线框全部进入磁场的过程中,通过截面的电量不相等 | |
| D. | 两线框全部进入磁场的过程中,消耗的电能之比为1:1 |
4.一列简谐横波沿x轴正方向传播,a﹑b为波上的两个质元,某时刻波形如图2所示,图2是从此时刻开始计时,a﹑b两个质元之一的振动图象,下列判断正确的是( )


| A. | 波速为10m/s,图2是质元b的振动图象 | |
| B. | 波速为10m/s,图2是质元a的振动图象 | |
| C. | 波速为12.5m/s,图2是质元b的振动图象 | |
| D. | 波速为12.5m/s,图2是质元a的振动图象 |
 某同学在进行“研究平抛物体的运动”实验:
某同学在进行“研究平抛物体的运动”实验: 如图1所示,竖直平面内有不计电阻、宽L=1m的∩型光滑金属框架,其上部分有一个正方形的区域存在随时间变化的匀强磁场B,B-t图如图2所示(垂直框架向里为磁场的正方向).框架下部分有一个虚线所示的区域有垂直框架平面向里的匀强磁场B0=1T,一根质量为m、电阻r=1Ω的金属棒ab跨放框架上与框架接触良好,在第1s内,金属棒恰好能静止.
如图1所示,竖直平面内有不计电阻、宽L=1m的∩型光滑金属框架,其上部分有一个正方形的区域存在随时间变化的匀强磁场B,B-t图如图2所示(垂直框架向里为磁场的正方向).框架下部分有一个虚线所示的区域有垂直框架平面向里的匀强磁场B0=1T,一根质量为m、电阻r=1Ω的金属棒ab跨放框架上与框架接触良好,在第1s内,金属棒恰好能静止.