��Ŀ����
����Ŀ����ͼ��ʾ�������ֱ�Ϊm��M����������A��B�����������¶���O��������Բ���˶�������A��B��������֮�����ΪL����֪A��B�����ĺ�O����ʼ�չ��ߣ�A��B�ֱ���O�����ࡣ��������ΪG
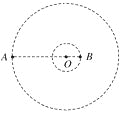
(1)����������Բ���˶������ڣ�
(2)�ڵ���ϵͳ�У����������������Ӱ�죬���Խ�����͵�����������A��B �� �����������������е����ڼ�ΪT1�����ڽ��ƴ�������ʱ��������Ϊ�������Ƶ�����Բ���˶��ģ�������õ��������ڼ�ΪT2����֪���������������ֱ�Ϊ5.98��1024kg��7.35��1022kg����T2��T1����ƽ��֮�ȡ������������λС����
���𰸡���1��T=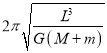 (2)
(2) ![]()
����������1��A��B��O������Բ���˶�������֮������������ṩ����������A��B����������С��ȣ���A��B��Oʼ�չ��ߣ�˵��A��B����ͬ�Ľ��ٶȺ����ڣ�����У�
m��2r��M��2R��r+R��L
������ã�R��![]() L��r��
L��r��![]() L
L
��A����ţ�ٵڶ����ɺ������������ɵã� ![]()
����ã�T��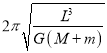
��2�������¿���˫�ǣ��ɣ�1����T1��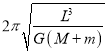
���������Ƶ�����Բ���˶�������ţ�ٵڶ����ɺ������������ɵã� ![]()
����ã� ![]()
�����������ڵ�ƽ����ֵΪ