题目内容
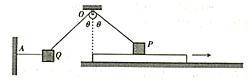
【题目】如图所示，小球A系在细线的一端，线的另一端固定在O点，O点到水平面的距离为h。物块B质量是小球的5倍，置于粗糙的水平面上且位于O点正下方，物块与水平面间的动摩擦因数为μ。现拉动小球使线水平伸直，小球由静止开始释放，运动到最低点时与物块发生正碰（碰撞时间极短），反弹后上升至最高点时到水平面的距离为h/4。小球与物块均视为质点，不计空气阻力，重力加速度为g，求：
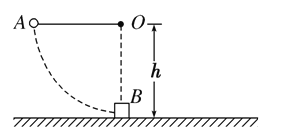
（1）小球运动到最低点与物块碰撞前的速度；
（2）碰撞结束时小球及物块的速度；
（3）物块在水平面上滑行的距离。
【答案】（1）
（2）
（3）
【解析】
设小球的质量为m，运动到最低点与物块碰撞前的速度大小为v1，取小球运动到最低点的重力势能为零，根据机械能守恒定律，有
mgh＝
mv12
得v1＝
设碰撞后小球反弹的速度大小为v1′，同理有
mg
＝mv12′
得v1′＝
设碰撞后物块的速度大小为v2，取水平向右的方向为正方向，
根据动量守恒定律，有mv1＝－mv1′＋5mv2
得v2＝
物块在水平面上滑行所受摩擦力的大小为
F＝5μmg
设物块在水平面上滑行的时间为t，根据动量定理，有
－Ft＝0－5mv2
得t＝
本题考查动量守恒定律和动量定理，由机械能守恒求出在最低点的速度，碰撞后的速度，碰撞前后动量守恒，列式求解
练习册系列答案
相关题目
