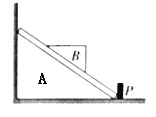
��Ŀ����
����Ŀ����ͼ��ʾ������Ϊm=2kg�����������Ϊ��=37���б�����ϣ�б������ΪM=4kg������⻬���ֶ�б����ʩһˮƽ����F��Ҫʹ���m���б�澲ֹ����ȡsin37��=0.6��cos37��=0.8��g=10m/s2��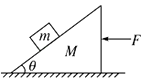
��1����б����������Ħ��������m���ٶȵĴ�С��m�ܵ�֧�����Ĵ�С��
��2����б��������Ķ�Ħ������Ϊ��=0.2����֪�������ܻ���Ħ���������Ħ������ȣ�������F��ȡֵ�������ʽ��С�������һλ��
���𰸡�
��1���⣺�����������ã������������б�������֧������������ˮƽ����

����ţ�ٵڶ����ɵã�
mgtan��=ma
�� a=gtan��=10��tan37��=7.5m/s2
m�ܵ�֧���� FN= ![]() =
= ![]() N=25N
N=25N
��m���ٶȵĴ�С��7.5m/s2��m�ܵ�֧�����Ĵ�С��25N��
��2���⣺����鴦�����б�����»������ٽ�״̬ʱ������ΪF1����ʱ������������ͼ��ʾ��
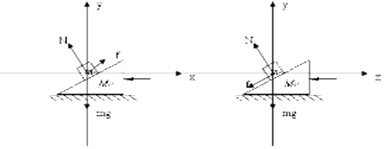
������������ˮƽ������ Nsin�ȩ���Ncos��=ma1
��ֱ������ Ncos��+��Nsin�ȩ�mg=0
�������� F1=��M+m��a1
������ֵ�� ![]() ��F1=28.8N
��F1=28.8N
����鴦�����б�����ϻ������ٽ�״̬ʱ������ΪF2��
������������ˮƽ������ N��sin����N��cos��=ma2
��ֱ������ N��sin�ȩ���N��sin�ȩ�mg=0
�������� F2=��M+m��a2
������ֵ�� ![]() ��F2=67.2N
��F2=67.2N
������������֪������F��ȡֵ��ΧΪ��28.8N��F��67.2N��
������F��ȡֵ��ΧΪ��28.8N��F��67.2N��
����������1��б��M�����m��ˮƽ����������һ�������ȼ����˶������m�ļ��ٶ�ˮƽ������ˮƽ���������m�������������ţ�ٵڶ����ɿ�������ٶ�a��֧��������2���ü�����F����������������������F��С��������0��ʱ�����ڦ̣�tan�ȣ������齫��б������»�����F�ϴ��㹻��ʱ����齫���б�����ϻ������F����̫С��Ҳ����̫����ţ�ٵڶ����ɣ�����������뷨���F��ȡֵ��Χ��

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�