题目内容
【题目】（10分）质量为4m的小物块A静止在离地面高h的水平桌面的边缘，质量为m的小物块B沿桌面向A运动以速度
与之发生正碰（碰撞时间极短）。碰后A离开桌面，其落地点离出发点的水平距离为L，碰后B反向运动。已知B与桌面间的动摩擦因数为μ，重力加速度为g，求：
(1)B后退的距离为多少？
(2)整个运动过程中，物块B克服摩擦力做的功与因碰撞损失的机械能之比为多少
【答案】（1）L24μh （2）14
【解析】
试题分析：设t为A从离开桌面至落地经历的时间，V表示刚碰后A的速度，有：
h=12gt2
L=vAt
解得：vA=Lg2h
设v为刚碰后B的速度的大小，由动量守恒定律得：
mv0=MvA-mv
由功能关系得：△E＝12mv2012×4mv2A12mv2
设B后退的距离为l，由动能定理得：
-μmgx=0-12mv2
由以上各式得：x=L24μh
（2）物块B克服摩擦力做的功等于B损失的动能，得：
Wf△E＝12mv2△E
代入数据得：Wf△E＝14
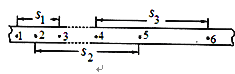
【题目】（10分）某同学利用电磁打点计时器打出的纸带验证机械能守恒定律，该同学在实验中得到一条纸带，如图所示，在纸带上取6个计数点，两个相邻计数点间的时间间隔为T=0.02s。其中1、2、3点相邻，4、5、6点相邻，在3点和4点之间还有若干个点。s1是1、3两点的距离，s2是2、5两点的距离，s3是4、6两点的距离。
（1）实验过程中，下列操作正确的是______ ___。
A．电磁打点计时器应接在220V交流电上 |
B．实验时应先松开纸带，然后迅速打开打点计时器 |
C．实验时应先打开打点计时器，然后松开纸带 |
D．纸带应理顺，穿过限位孔并保持竖直 |
（2）点2速度的表达式v2=___________。
（3）该同学测得的数据是s1=4.00cm，s2=16.00cm，s3=8.00cm，重物（质量为m）在竖直方向上运动从点2运动到点5过程中，动能增加量为______m，势能减少量为______m。（结果保留三位有效数字，重力加速度g =9.8m/s2）
