题目内容
3.如表记录了一竖直上抛运动的物体在空中运动时,位置与时刻的对应关系(取抛出点为原点O,向上为x轴的正方向,抛出时为零时刻),试证明重力加速度为g=$\frac{8({x}_{2}-{x}_{1})}{({t}_{4}-{t}_{1})^{2}-({t}_{3}-{t}_{2})^{2}}$.| t | t1 | t2 | t3 | t4 |
| x | x1 | x2 | x2 | x1 |
分析 物体做竖直上抛运动,运动过程具有对称性,由对称性可得到物体从x1与x2上升到最高点的时间,求出通过这两个位置的速度,再由速度位移关系公式求解.
解答 解:根据竖直上抛运动的对称性可知,物体从x1上升到最高点的时间为$\frac{{t}_{4}-{t}_{1}}{2}$,经过x1位置的速度大小为 v1=g•$\frac{{t}_{4}-{t}_{1}}{2}$;
物体从x2上升到最高点的时间为$\frac{{t}_{3}-{t}_{2}}{2}$,经过x2位置的速度大小为 v2=g•$\frac{{t}_{3}-{t}_{2}}{2}$;
从x2位置下落到x1位置,有:${v}_{1}^{2}-{v}_{2}^{2}$=2g(x2-x1)
联立得到 g=$\frac{8({x}_{2}-{x}_{1})}{({t}_{4}-{t}_{1})^{2}-({t}_{3}-{t}_{2})^{2}}$.
得证.
答:证明见上.
点评 对于竖直上抛运动,关键要灵活运用对称性,确定物体运动的时间,熟练运用运动学公式证明.

练习册系列答案
相关题目
13. 如图所示,两根粗糙金属导轨平行且均与水平面成θ角放置,轨道上方有一金属杆Q垂直于两导轨,金属杆Q的中点连一轻弹簧,弹簧另一端固定,弹簧处于伸长状态.导轨所在空间内存在垂直于导轨平面的匀强磁场,磁感应强度大小为B,方向如图所示.在导轨的下方另有一质量为m的金属杆P在一方向沿导轨向下的恒定外力F的作用下,从图示位置由静止开始下滑,金属杆P下滑距离x后最终以速度v匀速运动,弹簧长度始终保持不变.重力加速度为g,则( )
如图所示,两根粗糙金属导轨平行且均与水平面成θ角放置,轨道上方有一金属杆Q垂直于两导轨,金属杆Q的中点连一轻弹簧,弹簧另一端固定,弹簧处于伸长状态.导轨所在空间内存在垂直于导轨平面的匀强磁场,磁感应强度大小为B,方向如图所示.在导轨的下方另有一质量为m的金属杆P在一方向沿导轨向下的恒定外力F的作用下,从图示位置由静止开始下滑,金属杆P下滑距离x后最终以速度v匀速运动,弹簧长度始终保持不变.重力加速度为g,则( )
 如图所示,两根粗糙金属导轨平行且均与水平面成θ角放置,轨道上方有一金属杆Q垂直于两导轨,金属杆Q的中点连一轻弹簧,弹簧另一端固定,弹簧处于伸长状态.导轨所在空间内存在垂直于导轨平面的匀强磁场,磁感应强度大小为B,方向如图所示.在导轨的下方另有一质量为m的金属杆P在一方向沿导轨向下的恒定外力F的作用下,从图示位置由静止开始下滑,金属杆P下滑距离x后最终以速度v匀速运动,弹簧长度始终保持不变.重力加速度为g,则( )
如图所示,两根粗糙金属导轨平行且均与水平面成θ角放置,轨道上方有一金属杆Q垂直于两导轨,金属杆Q的中点连一轻弹簧,弹簧另一端固定,弹簧处于伸长状态.导轨所在空间内存在垂直于导轨平面的匀强磁场,磁感应强度大小为B,方向如图所示.在导轨的下方另有一质量为m的金属杆P在一方向沿导轨向下的恒定外力F的作用下,从图示位置由静止开始下滑,金属杆P下滑距离x后最终以速度v匀速运动,弹簧长度始终保持不变.重力加速度为g,则( )| A. | 金属杆P先做加速度减小的加速运动,最后匀速运动 | |
| B. | 金属杆Q的摩擦力先减小再增大 | |
| C. | 外力F的功是W=$\frac{1}{2}$mv2 | |
| D. | 回路产生的热量是Q=Fx+mgxsinθ-$\frac{1}{2}$mv2 |
14.下列说法正确的是( )
| A. | 半导体的导电性能介于导体与绝缘体之间,电阻随温度增加而增加 | |
| B. | 光敏电阻的特点是在光照下电阻大大减小 | |
| C. | 纯金属的电阻率随温度的升高而增加,可制成电阻温度计 | |
| D. | 热敏电阻的特点是其电阻随温度的升高而增加 |
12.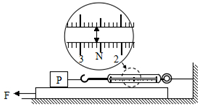 如图所示,把弹簧测力计的一端固定在墙上,用力F水平向左拉金属板,金属板向左运动,此时测力计的示数稳定(图中已把弹簧测力计的示数放大画出):
如图所示,把弹簧测力计的一端固定在墙上,用力F水平向左拉金属板,金属板向左运动,此时测力计的示数稳定(图中已把弹簧测力计的示数放大画出):
(1)此过程必须要匀速拉动木板,不能加速或者减速拉动吗?不是(填“是”或“不是”)
(2)则物块P与金属板间的滑动摩擦力的大小是2.60N,若用弹簧测力计测得物块P重13N,根据表中给出的动摩擦因数,可推算出物块P的材料为木头.
 如图所示,把弹簧测力计的一端固定在墙上,用力F水平向左拉金属板,金属板向左运动,此时测力计的示数稳定(图中已把弹簧测力计的示数放大画出):
如图所示,把弹簧测力计的一端固定在墙上,用力F水平向左拉金属板,金属板向左运动,此时测力计的示数稳定(图中已把弹簧测力计的示数放大画出):(1)此过程必须要匀速拉动木板,不能加速或者减速拉动吗?不是(填“是”或“不是”)
(2)则物块P与金属板间的滑动摩擦力的大小是2.60N,若用弹簧测力计测得物块P重13N,根据表中给出的动摩擦因数,可推算出物块P的材料为木头.
| 材料 | 动摩擦因数 |
| 金属-金属 | 0.25 |
| 橡胶-金属 | 0.30 |
| 木头-金属 | 0.20 |
| 皮革-金属 | 0.28 |
13.一个矩形线圈在匀强磁场中转动,产生的感应电动势按正弦规律变化,其瞬时值的表达式为e=220$\sqrt{2}$sin100πt,下列说法中正确的是( )
| A. | 频率是50Hz | B. | 当t=0时,线圈平面与中性面重合 | ||
| C. | 它的有效值为220V | D. | 它有最大值为220V |
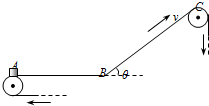 一传送带装置如图所示,其中AB段是水平的,长度LAB=4m,BC段是倾斜的,长度LBC=5m,倾角为θ=37°,AB和BC在B点通过一段极短的圆弧连接(图中未画出圆弧),传送带以v=4m/s的恒定速率顺时针运转.已知工件与传送带间的动摩擦因数μ=0.5,重力加速度g取10m/s2.现将一个工件(可看作质点)无初速地放在A点.求:(sin37°=0.6,cos37°=0.8)
一传送带装置如图所示,其中AB段是水平的,长度LAB=4m,BC段是倾斜的,长度LBC=5m,倾角为θ=37°,AB和BC在B点通过一段极短的圆弧连接(图中未画出圆弧),传送带以v=4m/s的恒定速率顺时针运转.已知工件与传送带间的动摩擦因数μ=0.5,重力加速度g取10m/s2.现将一个工件(可看作质点)无初速地放在A点.求:(sin37°=0.6,cos37°=0.8)