题目内容
20. 如图所示,可视为质点的物体分别沿斜面AB、DB顶端由静止下滑到底端,物体与AB、DB斜面之间的动摩擦因数相同,则( )
如图所示,可视为质点的物体分别沿斜面AB、DB顶端由静止下滑到底端,物体与AB、DB斜面之间的动摩擦因数相同,则( )| A. | 物体沿斜面DB滑动到底端时动能较大 | |
| B. | 物体沿斜面AB滑动到底端时动能较大 | |
| C. | 物体沿斜面DB滑动过程中克服摩擦力做的功较多 | |
| D. | 物体沿斜面AB滑动过程中克服摩擦力做的功较多 |
分析 根据动能定理得出末动能的大小,结合摩擦力做功的公式求出克服摩擦力做功,从而比较大小.
解答 解:设底边的长度为L,斜面的倾角为θ,根据动能定理得,mgh-$μmgcosθ•\frac{L}{cosθ}$=$\frac{1}{2}m{v}^{2}-0$,整理得,$mgh-μmgL=\frac{1}{2}m{v}^{2}$,知高度越高,到达底端的动能越大.
克服摩擦力做功${W}_{f}=μmgcosθ•\frac{L}{cosθ}=μmgL$,知克服摩擦力做功相等.故B正确,A、C、D错误.
故选:B.
点评 本题的关键是根据题意可以判定两个斜面的水平距离相等,设角度通过共同的物理量表示所要求的物理量,结合数学知识解答.

练习册系列答案
相关题目
15.飞机在高空水平匀速飞行,某时刻自由释放a球,1s后又自由释放b球,不计空气阻力,两球在落地前( )
| A. | a球在b球的前下方 | |
| B. | a球在b球的后下方 | |
| C. | a球始终在b球的正下方5m处 | |
| D. | a球始终在b球的正下方,但两者之间的距离逐渐变大 |
12.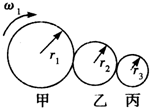 如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )
如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )
 如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )
如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )| A. | $\frac{{r}_{1}{ω}_{1}}{{r}_{3}}$ | B. | $\frac{{r}_{3}{ω}_{3}}{{r}_{1}}$ | C. | $\frac{{r}_{3}{ω}_{1}}{{r}_{2}}$ | D. | $\frac{{r}_{1}{ω}_{1}}{{r}_{2}}$ |
9. 6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )
6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )
 6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )
6月9日下午,嫦娥二号卫星正式飞离月球,其目的地是距离地球150万公里以外的日地拉格朗日L2点,如图所示.拉格朗日L2点在空间上有这样一个特点:它们绕太阳做周期性运动,但与地球和太阳之间的相对位置关系是保持不变的.利用L2可以保持背向太阳和地球、跟太阳和地球的相对“固定”的位置优势,可以安排天文望远镜和类似的观测设备,易于保护和校准.结合以上材料,请判定当嫦娥二号卫星处在L2点上时的相关说法正确的是( )| A. | 与地球具有相同的公转周期 | |
| B. | 公转线速度比地球的小 | |
| C. | 向心加速度比地球的小 | |
| D. | 设L2点到太阳的距离为R1,地球到太阳的距离为R2,周期分别为T1、T2,则$\frac{{R}_{1}^{3}}{{T}_{1}^{2}}$=$\frac{{R}_{2}^{3}}{{T}_{2}^{2}}$ |
 某同学用如图甲所示电路描绘一个“2.8V、1.5W”的小灯泡的伏安特性曲线,并将实验中得到的数据描在图乙所示的I-U坐标系中.
某同学用如图甲所示电路描绘一个“2.8V、1.5W”的小灯泡的伏安特性曲线,并将实验中得到的数据描在图乙所示的I-U坐标系中.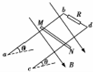 如图所示,间距为L的两根平行长直金属导轨ab、cd与水平面的夹角为θ,导轨上端接有阻值为R的电阻.一根电阻为3R的均匀直导体棒MN垂直放在两导轨上.整个装置处于方向垂直斜面向下、磁感应强度大小为B的匀强磁场中,MN由静止释放后沿导轨运动,位移大小为s时开始以最大速度vm做匀速运动.MN在运动过程中与导轨接触良好,导轨电阻及一切摩擦均不计,重力加速度大小为g.求:
如图所示,间距为L的两根平行长直金属导轨ab、cd与水平面的夹角为θ,导轨上端接有阻值为R的电阻.一根电阻为3R的均匀直导体棒MN垂直放在两导轨上.整个装置处于方向垂直斜面向下、磁感应强度大小为B的匀强磁场中,MN由静止释放后沿导轨运动,位移大小为s时开始以最大速度vm做匀速运动.MN在运动过程中与导轨接触良好,导轨电阻及一切摩擦均不计,重力加速度大小为g.求: 如图所示,在验证机械能守恒定律的实验中,下面列出了该实验的几个步骤,其中没有必要进行的步骤是C,操作不当的步骤是BD.(将选项前面的字母填在横线上)
如图所示,在验证机械能守恒定律的实验中,下面列出了该实验的几个步骤,其中没有必要进行的步骤是C,操作不当的步骤是BD.(将选项前面的字母填在横线上) 如图所示,AB为四分之一光滑圆弧轨道,半径R=0.8m,BC是水平轨道.物块(可视为质点)从A点由静止开始下滑,物块最终停在水平轨道上C点,若物块与BC间的动摩擦因数μ=0.8,求:
如图所示,AB为四分之一光滑圆弧轨道,半径R=0.8m,BC是水平轨道.物块(可视为质点)从A点由静止开始下滑,物块最终停在水平轨道上C点,若物块与BC间的动摩擦因数μ=0.8,求: 如图(甲)所示,在矩形线框的区域内存在着匀强磁场,开始时磁场垂直于纸面向内.已知磁场的磁感应强度B按图(乙)所示的规律变化,则线框中的感应电流I(取逆时针方向为正方向)随时间t变化的图象是( )
如图(甲)所示,在矩形线框的区域内存在着匀强磁场,开始时磁场垂直于纸面向内.已知磁场的磁感应强度B按图(乙)所示的规律变化,则线框中的感应电流I(取逆时针方向为正方向)随时间t变化的图象是( )


