题目内容
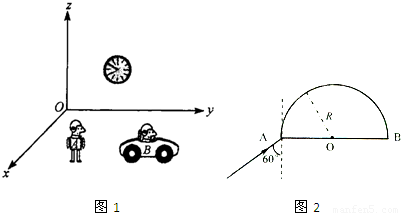
 (1)如图所示,竖直墙上挂着一面时钟,地面上静止的观察者A观察到钟的面积为S,另一观察者B以0.8倍光速平行y轴正方向运动,观察到钟的面积为S′.则S
(1)如图所示,竖直墙上挂着一面时钟,地面上静止的观察者A观察到钟的面积为S,另一观察者B以0.8倍光速平行y轴正方向运动,观察到钟的面积为S′.则S大于
大于
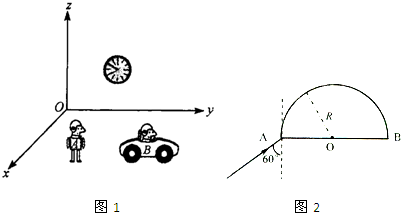
S′.(填“大于”、“等于”或“小于”)(2)一底面半径为R的半圆柱形透明体的折射率为n=
| 3 |
| ||
| 3 |
分析:(1)观察者B以0.8倍光速平行y轴正方向运动,根据爱因斯坦的相对论可知,B观察到的钟沿y轴方向的直径减小,而z轴方向的直径不变,钟的面积将与静止的观察者看到的面积要小.
(2)根据sinC=
,求出临界角.由折射定律求出折射角,判断光线折射后射到圆弧上时能否发生全反射,画出光路图,由几何知识求出在透明体内的路程s,光在光在透明体内的速度为v=
,由t=
求出时间.
(2)根据sinC=
| 1 |
| n |
| c |
| n |
| s |
| v |
解答:解:(1)观察者B以0.8倍光速平行y轴正方向运动,根据爱因斯坦的相对论尺缩效应可知,B观察到的钟沿y轴方向的直径将减小,而沿z轴方向的直径不变,钟的面积将与静止的观察者看到的面积要小,即S大于S′.
(2)设此透明物体的临界角为C,
依题意sinC=
,所以C=35°
当入射角为60°时,由n=
得到折射角:γ=30°

光线折射后射到圆弧上的C点,在C点的入射角为60°,大于临界角,会发生全反射
往后光线水平反射至圆弧上的D点并在D点发生全反射,再反射至B点,从B点第一次射出.
在透明体内的路径长为:s=3R
光在透明体内的速度v=
经历的时间 t=
=
故答案为:(1)大于;(2)该光线从进入透明体到第一次离开透明体时,共经历的时间为
.
(2)设此透明物体的临界角为C,
依题意sinC=
| 1 |
| n |
当入射角为60°时,由n=
| sin60° |
| sinγ |
得到折射角:γ=30°

光线折射后射到圆弧上的C点,在C点的入射角为60°,大于临界角,会发生全反射
往后光线水平反射至圆弧上的D点并在D点发生全反射,再反射至B点,从B点第一次射出.
在透明体内的路径长为:s=3R
光在透明体内的速度v=
| c |
| n |
经历的时间 t=
| s |
| v |
| 3nR |
| c |
故答案为:(1)大于;(2)该光线从进入透明体到第一次离开透明体时,共经历的时间为
| 3nR |
| v |
点评:第1题只要掌握相对论尺缩效应,就能判断出观察者B观察到钟的面积为S′小于S.对于几何光学,判断能否发生全反射是判断光线路径必须考虑的内容.

练习册系列答案
相关题目
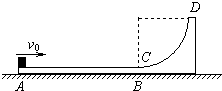 如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上.一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点.已知水平轨道AB长为L.求:(注意:图中v0是未知的)
如图所示,竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成,AB恰与圆弧CD在C点相切,轨道固定在水平面上.一个质量为m的小物块(可视为质点)从轨道的A端以初动能E冲上水平轨道AB,沿着轨道运动,由DC弧滑下后停在水平轨道AB的中点.已知水平轨道AB长为L.求:(注意:图中v0是未知的)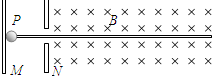 如图所示,竖直放置的金属薄板M、N间距为d.绝缘水平直杆左端从N板中央的小孔穿过,与M板固接,右端处在磁感应强度为B的匀强磁场中.质量为m、带电量为+q的中空小球P,套在水平直杆上,紧靠M板放置,与杆的动摩擦因数为μ.当在M、N板间加上适当的电压U后,P球将沿水平直杆从N板小孔射出,试问:
如图所示,竖直放置的金属薄板M、N间距为d.绝缘水平直杆左端从N板中央的小孔穿过,与M板固接,右端处在磁感应强度为B的匀强磁场中.质量为m、带电量为+q的中空小球P,套在水平直杆上,紧靠M板放置,与杆的动摩擦因数为μ.当在M、N板间加上适当的电压U后,P球将沿水平直杆从N板小孔射出,试问: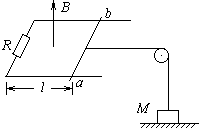 如图所示,竖直向上的匀强磁场,磁感应强度B=0.5T,并且以
如图所示,竖直向上的匀强磁场,磁感应强度B=0.5T,并且以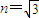 ,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,求:该光线从进入透明体到第一次离开透明体时,共经历的时间(已知真空中的光速为c,
,横截面如图所示,O表示半圆柱形截面的圆心.一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,求:该光线从进入透明体到第一次离开透明体时,共经历的时间(已知真空中的光速为c,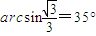 ;计算结果用R、n、c表示).
;计算结果用R、n、c表示).