Question

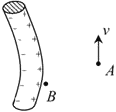
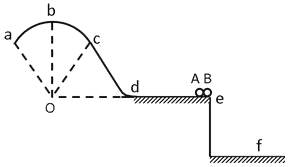
【题目】如图，竖直固定轨道abcd段光滑，长为L=1．0m的平台de段粗糙，abc段是以O为圆心的圆弧．小球A和B紧靠一起静止于e处，B的质量是A的4倍．两小球在内力作用下突然分离，A分离后向左始终沿轨道运动, 与de段的动摩擦因数μ=0．2，到b点时轨道对A的支持力等于A的重力的, B分离后平抛落到f点，f到平台边缘的水平距离S= 0．4m,平台高h=0．8m，g取10m/s2，求：

（1）AB分离时B的速度大小vB；

（2）A到达d点时的速度大小vd；

（3）圆弧 abc的半径R．

Answer 1

【答案】（1）vB="1" m/s （2）vd= 2 m/s （3）R=0．5m

【解析】

（1）解: （1）B分离后做平抛运动,由平抛运动规律可知:

h=gt2vB="s/t" 代入数据得:vB="1" m/s

（2）AB分离时，由动量守恒定律得：

mAve=mBvB A球由 e到d根据动能定理得:

-μmAgl=mAvd2-mAve2 代入数据得:vd= 2m/s

（3）A球由d到b根据机械能守恒定律得:

mAgR+mAvb2=mAvd2 A球在b由牛顿第二定律得:

mAg- mAg=mAvb2/R

代入数据得:R=0．5m