Question

(19 分）如图所示，正方形单匝均匀线框abcd,边长L=0.4m，每边电阻相等，总电阻R=0.5Ω。 一根足够长的绝缘轻质细线跨过两个轻质光滑定滑轮，一端连接正方形线框，另一端连接绝缘物体P,物体P放在一个光滑的足够长的固定斜面上，斜面倾角θ=30°,斜面上方的细线与斜面平行。在正方形线框正下方有一有界的勻强磁场，上边界I和下边界II都水平， 两边界之间距离也是L=0.4m。磁场方向水平，垂直纸面向里，磁感应强度大小B=0.5T。 现让正方形线框的cd边距上边界I的正上方高度h=0.9m的位置由静止释放，且线框在运动过程中始终与磁场垂直，cd边始终保持水平，物体P始终在斜面上运动，线框刚好能 以v =3m/_S的速度进入勻强磁场并匀速通过匀强磁场区域。释放前细线绷紧，重力加速度 g=10m/s²,不计空气阻力。

(1)线框的cd边在匀强磁场中运动的过程中，c、d间的电压是多大？

(2)线框的质量m₁和物体P的质量m₂分别是多大？

(3)在cd边刚进入磁场时，给线框施加一个竖直向下的拉力F使线框以进入磁场前的加速度匀加速通过磁场区域，在此过程中，力F做功W=0.23J,求正方形线框cd边产生的焦耳热是多少？

 

Answer 1

【答案】

(1) U_cd＝0.45V  (2)m₁＝0.032kg，m₂＝0.016kg   (3)Q_cd＝0.0575J

【解析】

试题分析：(1)正方形线框匀速通过匀强磁场区域的过程中，设cd边上的感应电动势为E，线框中的电流强度为I，c、d间的电压为U_cd，则

E＝BLv

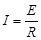
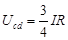
解得U_cd＝0.45V

(2)正方形线框匀速通过磁场区域的过程中，设受到的安培力为F，细线上的张力为T，则

F＝BIL

T＝m₂gsinθ

m₁g＝T＋F

正方形线框在进入磁场之前的运动过程中，根据能量守恒有

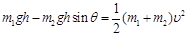
解得m₁＝0.032kg，m₂＝0.016kg

(3)因为线框在磁场中运动的加速度与进入前的加速度相同，所以在通过磁场区域的过程中，线框和物体P的总机械能保持不变，故力F做功W等于整个线框中产生的焦耳热Q，即

W=Q

设线框cd边产生的焦耳热为Q_cd，根据Q =I²Rt有

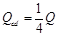
解得Q_cd＝0.0575J

考点：电磁感应   欧姆定律 焦耳定律 共点力平衡  能量守恒