��Ŀ����
����Ŀ����ͼ������Ϊ6m����ΪL�ı�ľ��AB���ڹ⻬��ˮƽ̨���ϣ�ľ��B����̨���ұ�Ե��ƽ��B���Ϸ�������Ϊ3m�ҿ���Ϊ�ʵ�Ļ���C��C��ľ��֮��Ķ�Ħ������Ϊ����![]() ������Ϊm��С���ó�ΪL��ϸ��������ƽ̨�ұ�Ե���Ϸ���O�㣬ϸ����ֱʱС��ǡ����C�Ӵ����ֽ�С����������ϸ��ˮƽ���ɾ�ֹ�ͷţ�С���˶�����͵�ʱϸ��ǡ�ö��ѣ�С����C����������Ϊ��ǰ��һ�롣
������Ϊm��С���ó�ΪL��ϸ��������ƽ̨�ұ�Ե���Ϸ���O�㣬ϸ����ֱʱС��ǡ����C�Ӵ����ֽ�С����������ϸ��ˮƽ���ɾ�ֹ�ͷţ�С���˶�����͵�ʱϸ��ǡ�ö��ѣ�С����C����������Ϊ��ǰ��һ�롣

����ϸ�����ܵ����������
����ҪʹС�������ͷŵ�����·�P�㣬ƽ̨�߶�ӦΪ���
��ͨ�������ж�C�ܷ��ľ���ϵ�������
���𰸡���1��3mg ��2��h��L��3��![]()
����������1����С���˶�����͵������Ϊv0��С�����°ڶ����̣�
�ɶ��ܶ���![]() ��
��![]()
С����Բ���˶���͵�ʱ���������ţ�ٵڶ����ɣ� ![]() ����ã�
����ã� ![]()
��ţ�ٵ������ɿ�֪��С���ϸ��������![]()
��2��С����ײ����ƽ���˶���
��ֱ��λ��![]()
ˮƽ��λ�ƣ� ![]()
��: ![]()
��3��С���뻬��C��ײ������С���Cϵͳ���㶯���غ㣬��C��������Ϊv1������������
![]()
����ľ���㹻������C��ľ����Ի���ֱ����Ծ�ֹ���̣����������չ�ͬ����Ϊv2��
�ɶ����غ㣺 ![]()
�������غ㣺 ![]()
������ã� ![]()
�������ľ���ϵ�����
��������������ǣ���1��![]() ��2��
��2��![]() ��3�����������
��3�����������

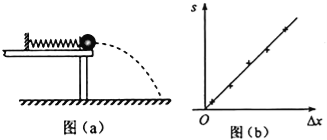
����Ŀ��ijͬѧ��������װ�ö����ʵ��ɵĵ������ܽ���̽����һ���ʵ��ɷ����ڹ⻬ˮƽ�����ϣ�������˹̶����Ҷ���һС��Ӵ��������������ɴ���ԭ��ʱ��С��ǡ���������Ե����ͼ��a����ʾ��������С��ʹ����ѹ��һ�ξ�����ɾ�ֹ�ͷţ�С���뿪������䵽ˮƽ���森ͨ�������ͼ��㣬����õ��ɱ�ѹ����ĵ������ܣ��ش��������⣺
��1����ʵ���п���Ϊ�����ɱ�ѹ����ĵ�������Ep��С���׳�ʱ�Ķ���Ek��ȣ���֪�������ٶȴ�СΪg��Ϊ���Ek��������Ҫ���������������е� ������ȷ�𰸱�ţ���
A���������m |
B��С���׳��㵽��ص��ˮƽ����s |
C�����浽����ĸ߶�h |
D�����ɵ�ѹ������x |
E������ԭ��l0
��2������ѡȡ�IJ���������֪����ʾEk����Ek= ��
��3��ͼ��b���е�ֱ����ʵ������õ���s����xͼ�ߣ��������Ͽ��Ƴ������h���䣮m���ӣ�s����xͼ�ߵ�б�ʻ� ������������������С�������������������m���䣬h���ӣ�s����xͼ�ߵ�б�ʻ� ������������������С������������������ͼ��b�� �и�����ֱ�߹�ϵ��Ek�ı���ʽ��֪��Ep����x�� �η������ȣ�


