题目内容
11.质量为0.5kg的小球甲以3m/s的速度和原来静止在光滑水平面上的质量为1kg的小球乙发生正碰,碰后以1m/s的速度被反弹,则碰后两球的总动量是1.5kg•m/s,甲、乙两球的动量大小之比p1:p2=1:4.分析 碰撞过程中动量守恒,根据动量守恒定律即可求解碰撞后的速度,得到各个球的动量.
解答 解:以小球甲的初速度方向为正方向,由动量守恒定律得:
P初=P末
所以碰后甲乙两球的总动量:
P末=P初=m甲v甲=0.5×3kg•m/s=1.5kg•m/s
根据:
m甲v甲=m甲v′甲+m乙v乙
得:
v乙=0.5×(3+1)=2m/s
故甲、乙两球的动量大小之比:
p1:p2=|m甲v′甲|:m乙v乙=0.5×1:1×2=1:4
故答案为:1.5,1:4.
点评 本题是动量守恒定律的简单应用,注意动量的矢量性,要先规定正方向,难度不大,属于基础题.

练习册系列答案
相关题目
1.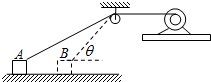 电动机以恒定的功率P和恒定的转速n卷动绳子,拉着质量为M的木箱在光滑的水平地面上前进,如图所示,当运动至绳子与水平面成θ角时,电动机的轮子卷绕绳子的半径为R,下述说法正确的是( )
电动机以恒定的功率P和恒定的转速n卷动绳子,拉着质量为M的木箱在光滑的水平地面上前进,如图所示,当运动至绳子与水平面成θ角时,电动机的轮子卷绕绳子的半径为R,下述说法正确的是( )
 电动机以恒定的功率P和恒定的转速n卷动绳子,拉着质量为M的木箱在光滑的水平地面上前进,如图所示,当运动至绳子与水平面成θ角时,电动机的轮子卷绕绳子的半径为R,下述说法正确的是( )
电动机以恒定的功率P和恒定的转速n卷动绳子,拉着质量为M的木箱在光滑的水平地面上前进,如图所示,当运动至绳子与水平面成θ角时,电动机的轮子卷绕绳子的半径为R,下述说法正确的是( )| A. | 木箱将做匀速运动,速度是2πnR | |
| B. | 木箱将做变速运动,此时速度是$\frac{2πnR}{cosθ}$ | |
| C. | 此时木箱对地的压力为Mg-$\frac{Psinθ}{2πnR}$ | |
| D. | 此过程木箱受的合外力大小和方向都在变化 |
2. 如图所示,足够长的光滑平行金属导轨与水平面成60°角倾斜放置于竖直向上的匀强磁场中,导轨间距为L,磁感应强度为B,其上端连接一个定值电阻R,将质量为m,长度也为L的金属棒ab在导轨上由静止释放,ab的电阻为r,其他电阻不计,当导体棒下滑位移为x时,恰好达到最大速度,导体版下滑过程中始终与导轨接触良好,重力加速度为g,不计空气阻力,则在该过程中( )
如图所示,足够长的光滑平行金属导轨与水平面成60°角倾斜放置于竖直向上的匀强磁场中,导轨间距为L,磁感应强度为B,其上端连接一个定值电阻R,将质量为m,长度也为L的金属棒ab在导轨上由静止释放,ab的电阻为r,其他电阻不计,当导体棒下滑位移为x时,恰好达到最大速度,导体版下滑过程中始终与导轨接触良好,重力加速度为g,不计空气阻力,则在该过程中( )
 如图所示,足够长的光滑平行金属导轨与水平面成60°角倾斜放置于竖直向上的匀强磁场中,导轨间距为L,磁感应强度为B,其上端连接一个定值电阻R,将质量为m,长度也为L的金属棒ab在导轨上由静止释放,ab的电阻为r,其他电阻不计,当导体棒下滑位移为x时,恰好达到最大速度,导体版下滑过程中始终与导轨接触良好,重力加速度为g,不计空气阻力,则在该过程中( )
如图所示,足够长的光滑平行金属导轨与水平面成60°角倾斜放置于竖直向上的匀强磁场中,导轨间距为L,磁感应强度为B,其上端连接一个定值电阻R,将质量为m,长度也为L的金属棒ab在导轨上由静止释放,ab的电阻为r,其他电阻不计,当导体棒下滑位移为x时,恰好达到最大速度,导体版下滑过程中始终与导轨接触良好,重力加速度为g,不计空气阻力,则在该过程中( )| A. | 导体棒的最大速度为$\frac{2\sqrt{3}(R+r)}{{B}^{2}{L}^{2}}$mg | |
| B. | 导体棒机械能的减少量为$\frac{\sqrt{3}}{2}$mgx-$\frac{{m}^{3}{g}^{2}(R+r)^{2}}{{B}^{4}{L}^{4}}$ | |
| C. | 电阻R上产生的焦耳热为$\frac{\sqrt{3}Rmgx}{2(R+r)}$-$\frac{6{m}^{3}{g}^{2}R(R+r)}{{B}^{4}{L}^{4}}$ | |
| D. | 通过R的电荷量为$\frac{BLx}{2(R+r)}$ |
19.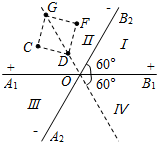 理论研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场,若均匀带电平面单位面积所带电荷量为σ,则产生匀强电场的电场强度的大小E=2πkσ,现有两块无限大的均匀绝缘带电平面,如图所示放置,A1B1两面带正电,A2B2两面带负电,且单位面积所带电荷量相等(设电荷不发生移动),A1B1面与A2B2面成60°,并且空间被分成了四个区间Ⅰ、Ⅱ、Ⅲ、Ⅳ,若区间Ⅰ、Ⅱ内的电场强度的大小分别为E1、E2,图中直线A1B1和A2B2分别为带正电平面和带负电平面与纸面正交的交线,O为两交线的交点,C、D、F、G恰好位于纸面内正方形的四个顶点上,且GD的连线过O点与带电平面均成60°夹角,则下列说法中正确的是( )
理论研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场,若均匀带电平面单位面积所带电荷量为σ,则产生匀强电场的电场强度的大小E=2πkσ,现有两块无限大的均匀绝缘带电平面,如图所示放置,A1B1两面带正电,A2B2两面带负电,且单位面积所带电荷量相等(设电荷不发生移动),A1B1面与A2B2面成60°,并且空间被分成了四个区间Ⅰ、Ⅱ、Ⅲ、Ⅳ,若区间Ⅰ、Ⅱ内的电场强度的大小分别为E1、E2,图中直线A1B1和A2B2分别为带正电平面和带负电平面与纸面正交的交线,O为两交线的交点,C、D、F、G恰好位于纸面内正方形的四个顶点上,且GD的连线过O点与带电平面均成60°夹角,则下列说法中正确的是( )
 理论研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场,若均匀带电平面单位面积所带电荷量为σ,则产生匀强电场的电场强度的大小E=2πkσ,现有两块无限大的均匀绝缘带电平面,如图所示放置,A1B1两面带正电,A2B2两面带负电,且单位面积所带电荷量相等(设电荷不发生移动),A1B1面与A2B2面成60°,并且空间被分成了四个区间Ⅰ、Ⅱ、Ⅲ、Ⅳ,若区间Ⅰ、Ⅱ内的电场强度的大小分别为E1、E2,图中直线A1B1和A2B2分别为带正电平面和带负电平面与纸面正交的交线,O为两交线的交点,C、D、F、G恰好位于纸面内正方形的四个顶点上,且GD的连线过O点与带电平面均成60°夹角,则下列说法中正确的是( )
理论研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场,若均匀带电平面单位面积所带电荷量为σ,则产生匀强电场的电场强度的大小E=2πkσ,现有两块无限大的均匀绝缘带电平面,如图所示放置,A1B1两面带正电,A2B2两面带负电,且单位面积所带电荷量相等(设电荷不发生移动),A1B1面与A2B2面成60°,并且空间被分成了四个区间Ⅰ、Ⅱ、Ⅲ、Ⅳ,若区间Ⅰ、Ⅱ内的电场强度的大小分别为E1、E2,图中直线A1B1和A2B2分别为带正电平面和带负电平面与纸面正交的交线,O为两交线的交点,C、D、F、G恰好位于纸面内正方形的四个顶点上,且GD的连线过O点与带电平面均成60°夹角,则下列说法中正确的是( )| A. | E1=E2 | |
| B. | E1=$\sqrt{3}$E2 | |
| C. | C、F两点电势相同 | |
| D. | 在C,D,F,G四个点中,电子在F点具有的电势能最大 |
6.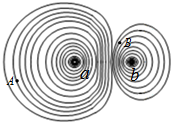 如图所示为真空中两个异种点电荷a、b电场的等势面分布,A、B为电场中的两点,且A点电势高于B点电势,则下列说法正确的是( )
如图所示为真空中两个异种点电荷a、b电场的等势面分布,A、B为电场中的两点,且A点电势高于B点电势,则下列说法正确的是( )
 如图所示为真空中两个异种点电荷a、b电场的等势面分布,A、B为电场中的两点,且A点电势高于B点电势,则下列说法正确的是( )
如图所示为真空中两个异种点电荷a、b电场的等势面分布,A、B为电场中的两点,且A点电势高于B点电势,则下列说法正确的是( )| A. | a带负电 | |
| B. | A的场强方向沿该处等势面的切线方向 | |
| C. | 同一检验电荷,在A点受到的电场力小于在B点受到的电场力 | |
| D. | 正检验电荷从A点移到B点,电势能增加 |
16. 如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m,下列说法正确的是( )
如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m,下列说法正确的是( )
 如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m,下列说法正确的是( )
如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m,下列说法正确的是( )| A. | 这列波沿x轴负方向传播 | |
| B. | 从该时刻开始d质点的位移随时间变化的函数关系为y=-5sin5πtcm | |
| C. | 经过$\frac{11}{30}$s时间b质点可能经过平衡位置且向下运动 | |
| D. | 经过$\frac{5}{30}$s时间b质点一定经过平衡位置且向下运动 |
20.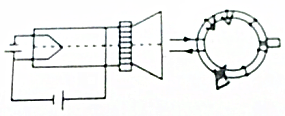 向荧光屏看去,电子向我们飞来,在偏转线圈中通以如图所示的电流,电子偏转方向为( )
向荧光屏看去,电子向我们飞来,在偏转线圈中通以如图所示的电流,电子偏转方向为( )
 向荧光屏看去,电子向我们飞来,在偏转线圈中通以如图所示的电流,电子偏转方向为( )
向荧光屏看去,电子向我们飞来,在偏转线圈中通以如图所示的电流,电子偏转方向为( )| A. | 向上 | B. | 向下 | C. | 向左 | D. | 向右 |
1.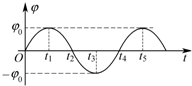 边长为a的N匝正方形线圈在匀强磁场中绕垂直于磁感线且与线圈在同一平面内的对称轴匀速转动,转速为n,线圈所围面积内的磁通量φ随时间t变化的规律如图所示,图象中φ0为已知.则下列说法中正确的是( )
边长为a的N匝正方形线圈在匀强磁场中绕垂直于磁感线且与线圈在同一平面内的对称轴匀速转动,转速为n,线圈所围面积内的磁通量φ随时间t变化的规律如图所示,图象中φ0为已知.则下列说法中正确的是( )
 边长为a的N匝正方形线圈在匀强磁场中绕垂直于磁感线且与线圈在同一平面内的对称轴匀速转动,转速为n,线圈所围面积内的磁通量φ随时间t变化的规律如图所示,图象中φ0为已知.则下列说法中正确的是( )
边长为a的N匝正方形线圈在匀强磁场中绕垂直于磁感线且与线圈在同一平面内的对称轴匀速转动,转速为n,线圈所围面积内的磁通量φ随时间t变化的规律如图所示,图象中φ0为已知.则下列说法中正确的是( )| A. | t1时刻线圈中感应电动势最大 | |
| B. | t2时刻线圈中感应电流为零 | |
| C. | 匀强磁场的磁感应强度大小为$\frac{φ_0}{{N{a^2}}}$ | |
| D. | 线圈中瞬时感应电动势的表达式为e=2Nπφ0ncos2πnt |
