题目内容
2. 如图所示,足够长的光滑平行金属导轨与水平面成60°角倾斜放置于竖直向上的匀强磁场中,导轨间距为L,磁感应强度为B,其上端连接一个定值电阻R,将质量为m,长度也为L的金属棒ab在导轨上由静止释放,ab的电阻为r,其他电阻不计,当导体棒下滑位移为x时,恰好达到最大速度,导体版下滑过程中始终与导轨接触良好,重力加速度为g,不计空气阻力,则在该过程中( )
如图所示,足够长的光滑平行金属导轨与水平面成60°角倾斜放置于竖直向上的匀强磁场中,导轨间距为L,磁感应强度为B,其上端连接一个定值电阻R,将质量为m,长度也为L的金属棒ab在导轨上由静止释放,ab的电阻为r,其他电阻不计,当导体棒下滑位移为x时,恰好达到最大速度,导体版下滑过程中始终与导轨接触良好,重力加速度为g,不计空气阻力,则在该过程中( )| A. | 导体棒的最大速度为$\frac{2\sqrt{3}(R+r)}{{B}^{2}{L}^{2}}$mg | |
| B. | 导体棒机械能的减少量为$\frac{\sqrt{3}}{2}$mgx-$\frac{{m}^{3}{g}^{2}(R+r)^{2}}{{B}^{4}{L}^{4}}$ | |
| C. | 电阻R上产生的焦耳热为$\frac{\sqrt{3}Rmgx}{2(R+r)}$-$\frac{6{m}^{3}{g}^{2}R(R+r)}{{B}^{4}{L}^{4}}$ | |
| D. | 通过R的电荷量为$\frac{BLx}{2(R+r)}$ |
分析 导体棒做匀速运动时速度最大,此时受力平衡,由平衡条件求解最大速度.根据动能与重力势能的变化分析机械能的减少量.由能量守恒求电阻R上产生的焦耳热.根据q=$\frac{△Φ}{R+r}$求解通过R的电荷量.
解答 解:A、导体棒做匀速运动时速度最大,设最大速度为v.
则 E=BLvcos60°,I=$\frac{E}{R+r}$,F安=BIL
根据平衡条件得 mgsin60°=F安cos60°,联立得v=$\frac{2\sqrt{3}(R+r)}{{B}^{2}{L}^{2}}$mg,故A正确.
B、导体棒机械能的减少量为△E=mgxsin60°-$\frac{1}{2}m{v}^{2}$=$\frac{\sqrt{3}}{2}$mgx-6$\frac{{m}^{3}{g}^{2}(R+r)^{2}}{{B}^{4}{L}^{4}}$,故B错误.
C、电阻R上产生的焦耳热为 Q=$\frac{R}{R+r}$△E=$\frac{\sqrt{3}Rmgx}{2(R+r)}$-$\frac{6{m}^{3}{g}^{2}R(R+r)}{{B}^{4}{L}^{4}}$,故C正确.
D、通过R的电荷量为 q=$\frac{△Φ}{R+r}$=$\frac{BLxcos60°}{R+r}$=$\frac{BLx}{2(R+r)}$,故D正确.
故选:ACD.
点评 正确推导出安培力与速度的关系、感应电荷量与位移的关系是解答本题的关键,要注意本题金属棒不是垂直切割磁感线,产生的感应电动势不是BLv,而要将速度分解得到有效切割速度vcos60°,感应电动势等于BLvcos60°.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.下列物体运动过程中,机械能守恒的是( )
| A. | 降落伞匀速下落 | B. | 汽车制动后在公路上滑行 | ||
| C. | 升降机加速上升 | D. | 小球做自由落体运动 |
10.水平地面上的物体重力为10N,外力F竖直向上作用于该物体,F的大小为3N,则地面对该物体支持力的大小是( )
| A. | 0N | B. | 3N | C. | 7N | D. | 10N |
7.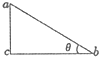 如图所示,在竖直平面内固定一光滑绝缘三角形支架,ac竖直、bc水平、ab与水平面夹角为θ,带电小球P和Q分别套在ab和ac上处于静止状态(P、Q均不与三角形支架顶点接触),设PQ连线与ab夹角为α,则下列判断正确的是( )
如图所示,在竖直平面内固定一光滑绝缘三角形支架,ac竖直、bc水平、ab与水平面夹角为θ,带电小球P和Q分别套在ab和ac上处于静止状态(P、Q均不与三角形支架顶点接触),设PQ连线与ab夹角为α,则下列判断正确的是( )
 如图所示,在竖直平面内固定一光滑绝缘三角形支架,ac竖直、bc水平、ab与水平面夹角为θ,带电小球P和Q分别套在ab和ac上处于静止状态(P、Q均不与三角形支架顶点接触),设PQ连线与ab夹角为α,则下列判断正确的是( )
如图所示,在竖直平面内固定一光滑绝缘三角形支架,ac竖直、bc水平、ab与水平面夹角为θ,带电小球P和Q分别套在ab和ac上处于静止状态(P、Q均不与三角形支架顶点接触),设PQ连线与ab夹角为α,则下列判断正确的是( )| A. | PQ可能带同种电荷 | B. | PQ一定带异种电荷 | ||
| C. | α可能小于θ | D. | α可能等于θ |
12.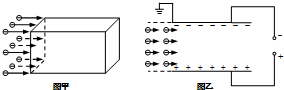 如图甲所示,某静电除尘装置中有一矩形通道,其前、后面板使用绝缘材料,上、下面板使用金属材料.图乙是装置的截面图,上、下两板与电压恒定的高压直流电源相连.带负电的尘埃水平进入矩形通道,当碰到下板后其所带电荷被中和,同时被收集.不计尘埃的重力.( )
如图甲所示,某静电除尘装置中有一矩形通道,其前、后面板使用绝缘材料,上、下面板使用金属材料.图乙是装置的截面图,上、下两板与电压恒定的高压直流电源相连.带负电的尘埃水平进入矩形通道,当碰到下板后其所带电荷被中和,同时被收集.不计尘埃的重力.( )
 如图甲所示,某静电除尘装置中有一矩形通道,其前、后面板使用绝缘材料,上、下面板使用金属材料.图乙是装置的截面图,上、下两板与电压恒定的高压直流电源相连.带负电的尘埃水平进入矩形通道,当碰到下板后其所带电荷被中和,同时被收集.不计尘埃的重力.( )
如图甲所示,某静电除尘装置中有一矩形通道,其前、后面板使用绝缘材料,上、下面板使用金属材料.图乙是装置的截面图,上、下两板与电压恒定的高压直流电源相连.带负电的尘埃水平进入矩形通道,当碰到下板后其所带电荷被中和,同时被收集.不计尘埃的重力.( )| A. | 电场力对尘埃做正功 | |
| B. | 尘埃的电势能变大 | |
| C. | 尘埃所受电场力的方向与电场方向相同 | |
| D. | 同一位置带电荷量越多的尘埃所受电场力越大 |
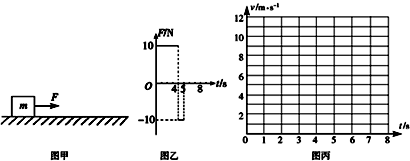
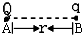 在真空中A点有一正电荷Q=2.0×10-4C,把检验电荷q=2.0×10-5C的负电荷置于B点,他们相距离r=2m,如图所示.求:
在真空中A点有一正电荷Q=2.0×10-4C,把检验电荷q=2.0×10-5C的负电荷置于B点,他们相距离r=2m,如图所示.求: