题目内容
16. 如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m,下列说法正确的是( )
如图所示是一列简谐横波在某时刻的波动图象,从该时刻开始,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s.若b质点的平衡位置为x=$\frac{4}{3}$m,下列说法正确的是( )| A. | 这列波沿x轴负方向传播 | |
| B. | 从该时刻开始d质点的位移随时间变化的函数关系为y=-5sin5πtcm | |
| C. | 经过$\frac{11}{30}$s时间b质点可能经过平衡位置且向下运动 | |
| D. | 经过$\frac{5}{30}$s时间b质点一定经过平衡位置且向下运动 |
分析 波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s,由次判断出质点的振动方向和波的传播方向,结合时间即可求出周期和频率.读出波长,即可写出质点的振动方程以及求出波速.根据平移法,分析状态关系.
解答 解:由题,此波中d质点第一次到达波谷的时间比e质点第一次到达波谷的时间早0.10s,结合题图可知质点d一定是正在向下运动,而且由于是经过$\frac{1}{4}$T到达最低点.所以该波振动的周期是T=4×0.1=0.4s.由题可知,该波的波长是4m.
A、质点d一定是正在向下运动,由题,结合平移法可知,该波沿x轴正方向传播.故A错误;
B、该波的周期是0.4s,角速度:$ω=\frac{2π}{T}=\frac{2π}{0.4}=5π$rad/s,由题可知,该波的振幅是5cm,质点d一定是正在向下运动,所以从该时刻开始d质点的位移随时间变化的函数关系为y=-5sin5πtcm.故B正确;
C、该波传播的速度:$v=\frac{λ}{T}=\frac{4}{0.4}=10$m/s.经过$\frac{11}{30}$s时间该波传播的距离是:△x1=vt1=$10×\frac{11}{30}=\frac{11}{3}$m,而$\frac{4}{3}-\frac{11}{3}=\frac{-7}{3}$m,即x=$-\frac{7}{3}$m处的振动传播到了b点,由图结合波的传播方向可知,x=-$\frac{7}{3}$m处的质点不过平衡位置.所以经过$\frac{11}{30}$s时间b质点不在平衡位置.故C错误;
D、经过$\frac{5}{30}$s时间该波传播的距离是:△x1=vt1=$10×\frac{5}{30}=\frac{5}{3}$m,而$\frac{4}{3}-\frac{5}{3}=-\frac{1}{3}$m,即x=-$\frac{1}{3}$m处的振动传播到了b点,由图结合波的传播方向可知,x=-$\frac{1}{3}$m处的质点不在平衡位置.所以经过$\frac{5}{30}$s时间b质点一定经过不在平衡位置.故D错误.
故选:B
点评 根据质点的振动状态确定周期与时间的关系、根据距离与波长的关系,分析质点状态关系是基本能力,要加强训练,熟练掌握.

 阅读快车系列答案
阅读快车系列答案| A. | 牛顿、卡文迪许 | B. | 伽利略、卡文迪许 | C. | 开普勒、牛顿 | D. | 第谷、伽利略 |
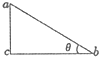 如图所示,在竖直平面内固定一光滑绝缘三角形支架,ac竖直、bc水平、ab与水平面夹角为θ,带电小球P和Q分别套在ab和ac上处于静止状态(P、Q均不与三角形支架顶点接触),设PQ连线与ab夹角为α,则下列判断正确的是( )
如图所示,在竖直平面内固定一光滑绝缘三角形支架,ac竖直、bc水平、ab与水平面夹角为θ,带电小球P和Q分别套在ab和ac上处于静止状态(P、Q均不与三角形支架顶点接触),设PQ连线与ab夹角为α,则下列判断正确的是( )| A. | PQ可能带同种电荷 | B. | PQ一定带异种电荷 | ||
| C. | α可能小于θ | D. | α可能等于θ |
| A. | 晶体都具有确定的熔点 | |
| B. | 空气相对湿度大,就是空气中水蒸气含量高 | |
| C. | 物体从外界吸收热量,其内能不一定增加 | |
| D. | 空调机在制冷过程中,从室内吸收的热量等于向室外放出的热量 |
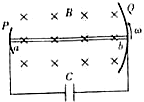 如图所示,在空间存在着竖直向下的匀强磁场,磁感应强度为B.一水平放置的长度为L的金属杆ab与圆弧形金属导轨P、Q紧密接触,P、Q之间接有电容为C的电容器.若ab杆绕a点以角速度ω沿逆时针方向匀速转动,则下列说法正确的是( )
如图所示,在空间存在着竖直向下的匀强磁场,磁感应强度为B.一水平放置的长度为L的金属杆ab与圆弧形金属导轨P、Q紧密接触,P、Q之间接有电容为C的电容器.若ab杆绕a点以角速度ω沿逆时针方向匀速转动,则下列说法正确的是( )| A. | 电容器与a相连的极板带正电 | B. | 电容器与b相连的极板带正电 | ||
| C. | 电容器的带电量是$\frac{CB{ω}^{2}L}{2}$ | D. | 电容器的带电量是$\frac{CBω{L}^{2}}{2}$ |
| A. | 鸟儿能欢快地停在高压电线上是因为鸟儿的脚上有一层绝缘皮 | |
| B. | 能量耗散表明能源在利用过程中能量不断消失,因此要节约能源 | |
| C. | 车辆在公路弯道不允许超过规定速度是防止因离心运动造成交通事故 | |
| D. | 开关断开时会出现电火花是因为电路中的线圈产生很大的自感电动势 |
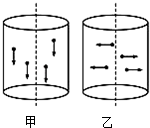 有同学想通过静电除尘的方法净化空气.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.方法一是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;方法二是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,不计尘埃的重力,则( )
有同学想通过静电除尘的方法净化空气.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.方法一是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;方法二是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,不计尘埃的重力,则( )| A. | 两种方法中尘粒最终一定都做匀速运动 | |
| B. | 两种方法下尘粒受到的电场力大小相等 | |
| C. | 电场对单个尘粒做功的最大值相等 | |
| D. | 乙容器中的尘粒不可能做匀速直线运动 |
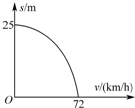 某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )
某司机在检测汽车性能过程中,得到汽车减速过程中的位移s与速度v的关系曲线如图所示,并得出位移s与速度v的函数关系式为s=m-nv2,其中m、n为常数.重力加速度的大小g取10m/s2.则以下判断正确的是( )| A. | 汽车在此过程中做匀变速直线运动 | |
| B. | 汽车的末速度为20m/s | |
| C. | 由题中所给已知条件可确定m、n的大小 | |
| D. | 汽车对司机作用力的大小与司机重力大小的比值为$\frac{4}{5}$ |