题目内容
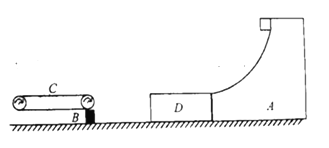
【题目】如图所示,右侧为固定的光滑圆弧导轨A,末端水平。左侧B为固定的挡板,C为足够长的传送带。以速度v=5m/s顺时针运动。D为下表面光滑的木板,质量为M=1kg,长度为L=3m。A的末端与C、D三者的上表面等高,最初D紧靠着A。一个质量为m=2kg的滑块(可看作质点)从A上由静止下滑高度h=1.8m后,滑上木板D。已知滑块恰能滑到木板D的左端,且此刻木板恰与B相撞,若木板与挡板、导轨每次碰撞后,速度均变为零(但不粘连),滑块与木板及传送带间的动摩擦因数都相等,g=10m/s2,D与B碰后C、D间的缝隙很小忽略不计。求:
(1)动摩擦因数;
(2)滑块第一次滑上传送带运动到最左端过程中,电动机对传送带多做的功;
(3)滑块第一次返回轨道A的最大高度。
【答案】(1)0.2 (2)40J (3)![]()
【解析】
(1)滑块滑下,根据动能定理:
![]()
解得:![]()
木板D和滑块组成的系统动量守恒:
![]()
由能量守恒可知滑块和木板D损失的动能转化为系统的摩擦生热:
![]()
联立可解得:![]() ,
,![]()
(2)电动机对传送带多做的功为摩擦生热减去滑块损失的动能,滑块在传送带向最左端运动的过程中做匀减速运动,最后减速到零,由牛顿第二定律可知:
![]()
解得:![]()
由运动学可知滑块在传送带运动的时间:
![]()
滑块的位移:
![]()
则传送带的位移:
![]()
系统摩擦生热为:
![]()
滑块损失的动能为:
![]()
则电动机多做的功:
![]()
(3)再次滑上木板:
![]()
滑块和木板再次损失的热量:
![]()
木板和导轨碰撞后滑块上升到最高点的过程:
![]()
联立解得:![]()

练习册系列答案
相关题目