题目内容

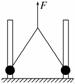
 如图3所示，两根相距L平行放置的光滑导轨，倾角为α，轨道间有电阻R，处于磁感应强度大小为B，方向竖直向上的匀强磁场中，一根质量为m、电阻为R/4的金属杆ab，由静止开始沿导轨下滑.设下滑中ab杆始终与轨道保持垂直，且接触良好，导轨足够长且电阻不计，求杆ab沿导轨下滑可达到的最终速度.


当ab杆沿导轨下滑时将产生感应电动势，ab杆与电阻R构成的回路内将产生感应电流，故ab杆将受到安培力的作用；当ab杆所受各力平衡时达到最终速度.设此时ab杆的速度为v，其受力情况如图4所示（注意正确判断安培力的方向）.
由三角知识可得ab杆切割磁感线的速度为v′=vcosα.
所以感应电动势为
E=BLv′
E=BLvcosα
由闭合电路欧姆定律有
I=E/（R+R/4）
则杆所受安培力为 FB=BIL
由力的平衡，有 mgsinα=FBcosα
综上可解得杆的最终速度为v=5mgRsinα/4B2L2cos2α
【试题分析】
【解析】当ab杆沿导轨下滑时将产生感应电动势，ab杆与电阻R构成的回路内将产生感应电流，故ab杆将受到安培力的作用；当ab杆所受各力平衡时达到最终速度.设此时ab杆的速度为v，其受力情况如图4所示（注意正确判断安培力的方向）.
由三角知识可得ab杆切割磁感线的速度为v′=vcosα.
所以感应电动势为
E=BLv′
E=BLvcosα
由闭合电路欧姆定律有
I=E/（R+R/4）
则杆所受安培力为 FB=BIL
由力的平衡，有 mgsinα=FBcosα
综上可解得杆的最终速度为v=5mgRsinα/4B2L2cos2α
练习册系列答案
相关题目
如图甲所示，两根相距为L的金属轨道固定于水平面上，导轨电阻不计，一根质量为m、长为L、电阻为R的金属棒两端放于导轨上，导轨与金属棒间的动摩擦因数为?，棒与导轨的接触电阻不计．导轨左端连有阻值为2R的电阻，在电阻两端接有电压传感器并与计算机相连．有n段竖直向下的宽度为a间距为b的匀强磁场（a＞b），磁感强度为B、金属棒初始位于OO′处，与第一段磁场相距2a．

（1）若金属棒有向右的初速度v0，为使金属棒保持v0一直向右穿过各磁场，需对金属棒施加一个水平向右的拉力，求金属棒进入磁场前拉力F1的大小和进入磁场后拉力F2的大小；
（2）在（1）的情况下，求金属棒从OO′开始运动到刚离开第n段磁场过程中，拉力所做的功；
（3）若金属棒初速为零，现对棒施以水平向右的恒定拉力F，使棒穿过各段磁场，发现计算机显示出的电压随时间以固定的周期做周期性变化，在给定的坐标图乙中定性地画出计算机显示的图象（从金属棒进入第一段磁场开始计时）．
（4）在（3）的情况下，求整个过程导轨左端电阻上产生的热量，以及金属棒从第n段磁场穿出时的速度．
（2013?日照一模）（1）某同学在研究“对不同物体做相同功情况下，物体质量与速度的关系”时，提出了以下四种猜想：
A．m∞υ
B．m∞
1
υ

C．m∞υ2
D.m∞
1
υ2

为验证猜想的正确性，该同学用如图1所示的装置进行实验：将长木板平放在水平桌面上，木块固定在长木板一端，打点计时器固定在木块上，木块右侧固定一轻弹簧，用连接纸带的小车压缩弹簧至长木板的虚线处由静止释放，打点计时器在纸带上打下一系列点，选取点迹均匀的一部分纸带，计算出小车匀速运动的速度υ1，测出小车的质量m1；然后在小车上加砝码，再次压缩弹簧至木板虚线处由静止释放小车，计算出小车和砝码匀速运动的速度υ2，测出小车和砝码的总质量m2：再在小车上加砝码，重复以上操作，分别测出υ3、m3…．

①每次实验中，都将小车压缩弹簧至长木板的虚线处由静止释放，目的是
小车获得相同的动能（弹簧对小车做功相同）
小车获得相同的动能（弹簧对小车做功相同）
；若要消除每次实验中小车和纸带受到的阻力对小车运动的影响，应进行的实验操作是
垫高木板固定打点计时器的一端，使小车连同纸带一起在木板上匀速运动（平衡摩擦力）
垫高木板固定打点计时器的一端，使小车连同纸带一起在木板上匀速运动（平衡摩擦力）
．
②某次实验采集的五组数据如表：由表格数据直观判断，明显不正确的两个猜想是A、B、C、D中的
AC
AC
；若对某个猜想进行数据处理并作图，画出了如图2所示的图象，则图中的横坐标应是
1
v2
1
v2
．
m/kg 0.10 0.20 0.30 0.40 0.50
v/（m?s-1） 1.000 0.707 0.577 0.500 0..447
（2）冬、春季节降水量少，广东沿海附近江河水位较低，涨潮时海水倒灌，出现“咸潮”现象，使沿海地区的城市自来水中的离子浓度增高，电阻率变小，水质受到影响．某同学设计了一个监测河水电阻率的实验．在一根均匀长度玻璃管两端分别装上橡胶塞和铂电极，如图3所示，两电极相距L=0.314m，管内充满待测的河水．安装前用游标卡尺测量玻璃管的内径，测量结果如图4所示．
为测管内河水电阻供选器材有：
电压表V1：量程15V，内阻约30kΩ
电压表V2：量程3V，内阻约10kΩ
电流表A1：量程0.6A，内阻约0.5Ω
电流表A2：量程150mA，内阻约10Ω
滑动变阻器甲：最大值为10Ω，额定电流足够大
滑动变阻器乙：最大值为1kΩ，额定电流足够大
电源E1：电动势15V，内阻6Ω
电源E2：电动势3V，内阻2Ω
开关、导线若干．
该同学选用以上部分器材测出了9组数据，并在坐标系中标出，如图5所示．
①据图（2）读出玻璃管的内径d=
6.70
6.70
mm．
②实验时，所选用的电压表为
V1
V1
（填“V1”或“V2”），所选用的电流表为
A2
A2
（填“A1”或“A2”），所选的滑动变阻器为
甲
甲
（填“甲”或“乙”），所选的电源为
E1
E1
（填“E1”或“E2”）．
③在答题卡的虚线框内画出该实验的原理图．

如图8所示，两根相距为L的竖直固定杆上各套有质量为m的小球，小球可以在杆上无摩擦地自由滑动，两小球用长为2L的轻绳相连，今在轻绳中点施加一个竖直向上的拉力F，恰能使两小球沿竖直杆向上匀速运动。则每个小球所受的拉力大小为(重力加速度为g)(　　)

图8

A.                                            B．mg

C.F/3                                 D．F

如图6所示，两根相距为L的竖直固定杆上各套有质量为m的小球，小球可以在杆上无摩擦地自由滑动，两球用长为2L的轻绳相连，今在轻绳中点施加一个竖直向上的拉力F，恰能使两球沿竖直杆向上匀速运动。则每个小球所受的拉力大小为(重力加速度为g)(　　)　　　　　　　　

A．mg/2 　　　　　　　　　　　　　　　　　　　　　　 B．mg

C.F/3 　　　　　　　　　　　　　　　　　　　　　　 D．F

图6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网