题目内容
如图所示,绝缘小球A静止在高为h="0.8" m的光滑平台上,带电量为qB =+0.3C的小球B用长为L=1m的细线悬挂在平台上方,两球质量mA=mB=0.5kg,整个装置放在竖直向下的匀强电场中,场强大小E =10N/C,现将细线拉开角度α =60o后,由静止释放B球,在最低点与A球发生对心碰撞,碰撞时无机械能损失。不计空气阻力,取g=10m/s2,求:
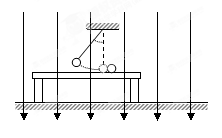
小题1:B球在碰撞前的速度;
小题2:A球离开平台的水平位移大小。

小题1:B球在碰撞前的速度;
小题2:A球离开平台的水平位移大小。
小题1:v0=4m/s
小题2:1.6m
(1)设B球在最低点速度为 ,碰撞前对B球由动能定理得:
,碰撞前对B球由动能定理得:
mBgL(1-cosα)+qBEL(1-cosα)= mB
mB (4分)
(4分)
解得: v0="4m/s " (2分)
(2)碰撞后A球B球速度分别为vA,vB,由动量守恒得:
mBv0=mBvB+mAvA (3分)
能量守恒: (3分)
(3分)
联立解得 vA="4m/s " (vB="0) " (2分)
碰后A先匀速运动,再平抛运动
竖直方向:
 (2分)
(2分)
水平位移s=vAt="4×0.4=1.6m " (2分)
 ,碰撞前对B球由动能定理得:
,碰撞前对B球由动能定理得: mBgL(1-cosα)+qBEL(1-cosα)=
 mB
mB (4分)
(4分)解得: v0="4m/s " (2分)
(2)碰撞后A球B球速度分别为vA,vB,由动量守恒得:
mBv0=mBvB+mAvA (3分)
能量守恒:
 (3分)
(3分)联立解得 vA="4m/s " (vB="0) " (2分)
碰后A先匀速运动,再平抛运动
竖直方向:

 (2分)
(2分)水平位移s=vAt="4×0.4=1.6m " (2分)

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目

 mg2t2
mg2t2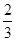 mg2t2
mg2t2
 的初速度,使之向右运动,在木板与木块向右运动过程中,当木板和
的初速度,使之向右运动,在木板与木块向右运动过程中,当木板和 木块达到共速时,木板恰与墙壁相碰,碰撞过程时间极短,木板速度的方向改变,大小不变,最后木块恰好在木板的左端与木板相对静止。求:
木块达到共速时,木板恰与墙壁相碰,碰撞过程时间极短,木板速度的方向改变,大小不变,最后木块恰好在木板的左端与木板相对静止。求:
 ;
; ;
;