题目内容
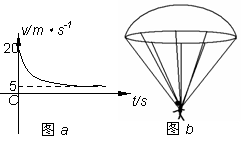
某运动员做跳伞训练，他从悬停在空中的直升飞机上由静止跳下，跳离飞机一段时间后打开降落伞做减速下落。他打开降落伞后的速度时间图象如图a（t=0为打开伞瞬间）。降落伞用8根对称的绳悬挂运动员，每根绳与中轴线的夹角均为37°，如图b。已知人的质量为50kg，降落伞质量也为50kg，不计人所受的空气阻力，打开伞后降落伞所受阻力f与速度v成正比，即f=kv (g取10m/s2，sin53°=0.8，cos53°=0.6) ．求：
（1）打开降落伞前人自由下落的距离；
（2）阻力系数k；
（3）打开伞瞬间加速度a的大小和方向以及此时每根悬绳承受的拉力为多少。
解析：（1）
（2分）
（2）
，
（2分）
（3） 对整体：
，
（2分）
方向竖直向上（1分）
设每根绳拉力为T，以运动员为研究对象有：
，
（2分）
由牛顿第三定律得：悬绳能承受的拉力为至少为312.5N （1分）
练习册系列答案
相关题目
某运动员做跳伞训练，他从悬停在空中的直升飞机上由静止跳下，跳离飞机一段时间后打开降落伞做减速下落，他打开降落伞后的速度图线如图a．降落伞用8 根对称的绳悬挂运动员，每根绳与中轴线的夹角均为37°，如图b．已知人的质量为50kg，降落伞质量也为50kg，不计人所受的阻力，打开伞后伞所受阻力f，与速度v成正比，即f=kv（g取10m/s2，sin53°=0.8，cos53°=0.6）．求：
某运动员做跳伞训练，他从悬停在空中的直升机上由静止跳下，跳离飞机一段时间后打开降落伞减速下落．他打开降落伞后的速度图线如图（a）所示．降落伞用8根对称的绳悬挂运动员，每根绳与中轴线的夹角均为 α=37°，如图（b）所示．已知运动员的质量为50kg，降落伞的质量也为50kg，不计运动员所受的阻力，打开伞后伞所受阻力f与速度v成正比，即f=kv（g取10m/s2，sin 37°=0.6．cos 37°=0.8）．则下列判断中正确的是（ ）
某运动员做跳伞训练，他从悬停在空中的直升机上由静止跳下，跳离飞机一段时间后打开降落伞做减速下落．他打开降落伞后的速度图线如图甲，降落伞用8根对称的绳悬挂运动员，绳与竖直中轴线的夹角θ=37°，如图乙．已知人的质量m=50kg，降落伞质量M=50kg，开伞前不计人所受的阻力，打开伞后伞所受阻力f与速率v成正比，即f=kv．已知sin53°=0.8，cos53°=0.6，取g=10m/s2．求：
