题目内容
4.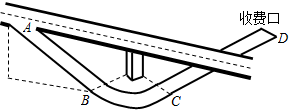 某高速公路的一个出口路段如图所示,情景简化:轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到D点停下.已知轿车在A点的速度v0=72km/h,AB长L1=l50m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=36km/h,轮胎与BC段路面间的动摩擦因数μ=0.5,最大静摩擦力可认为等于滑动摩擦力,CD段为平直路段长L2=50m,重力加速度g取l0m/s2.
某高速公路的一个出口路段如图所示,情景简化:轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到D点停下.已知轿车在A点的速度v0=72km/h,AB长L1=l50m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=36km/h,轮胎与BC段路面间的动摩擦因数μ=0.5,最大静摩擦力可认为等于滑动摩擦力,CD段为平直路段长L2=50m,重力加速度g取l0m/s2.(1)若轿车到达B点速度刚好为v=36km/h,求轿车在AB下坡段加速度的大小;
(2)为保证行车安全,车轮不打滑,求水平圆弧段BC半径R的最小值;
(3)轿车A点到D点全程的最短时间.
分析 (1)轿车在AB段做匀减速直线运动,已知初速度、位移和末速度,根据速度位移关系公式求解加速度.
(2)轿车在BC段做匀速圆周运动,由静摩擦力充当向心力,为保证行车安全,车轮不打滑,所需要的向心力不大于最大静摩擦力,据此列式求解半径R的最小值.
分三段,分别由运动学公式求解时间,即可得到总时间
解答 解:(1)v0=72km/h=20m/s,AB长L1=l50m,v=36km/h=10m/s,对AB段匀减速直线运动有
v2$-{v}_{0}^{2}$=-2aL1
代入数据解得 a=1m/s2
(2)汽车在BC段做圆周运动,静摩擦力提供向心力,
${F_f}=m\frac{v^2}{R}$
为了确保安全,则须满足 Ff≤μmg
联立解得:R≥20m,即:Rmin=20m
(3)设AB段时间为t1,BC段时间为t2,CD段时间为t3,全程所用最短时间为t.
L1=$\frac{{v}_{0}+v}{2}{t}_{1}$
$\frac{1}{2}π$R=vt2
L2=$\frac{v}{2}{t}_{3}$
t=t1+t2+t3
解得:t=23.14 s
答:(1)若轿车到达B点速度刚好为v=36km/h,轿车在AB下坡段加速度的大小为1m/s2;
(2)为保证行车安全,车轮不打滑,水平圆弧段BC半径R的最小值为20m;
(3)轿车A点到D点全程的最短时间为23.14 s.
点评 本题是运动学与动力学综合题,能结合物体的运动情况,灵活选择运动学的公式形式是关键,当不涉及加速度而要求时间时,可用位移等于平均速度乘以时间来求.

练习册系列答案
相关题目
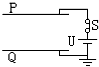
14.如图所示,P?Q为一平行板电容器的两个极板,其中Q板接地,下列说法正确的是( )

| A. | 适当上移P极板,电容器电容增大 | |
| B. | 保持开关S闭合,适当左移P极板,电容器电量增大 | |
| C. | 若断开开关S,再适当上移P极板,板间场强减小 | |
| D. | 若断开开关S,再适当左移P极板,P板电势升高 |
15.下列说法中正确的是( )
| A. | 气体压强的大小和单位体积内的分子数及气体分子的平均动能都有关 | |
| B. | 布朗运动是液体分子的运动,说明液体分子永不停息地做无规则热运动 | |
| C. | 热力学第二定律的开尔文表述:不可能从单一热库吸收热量,使之完全变成功,而不产生其他影响 | |
| D. | 水黾可以停在水面上是因为液体具有表面张力 | |
| E. | 温度升高,物体所有分子的动能都增大 |
12.某课外兴趣小组用铜片和锌片插入苹果中,组成了一个苹果电池,并用“测定电动势和内电阻”的实验方法测定该苹果电池的电动势和内电阻.
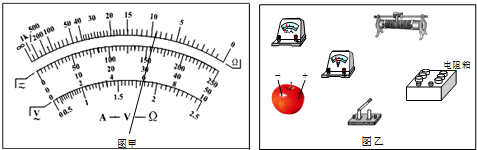
(1)实验前,甲同学利用调好的多用电表欧姆“×100”档来粗测该苹果电池的内阻.测量结果如图甲所示.他这样做是否正确?若正确,请读出其内阻值;若不正确,请说明理由.不正确 水果电池为电源,欧姆表不能电源的内阻.
(2)乙同学设计好测量电路,选择合适的器材,得到苹果电池两端的电压U和流过它的电流I的几组数据,如下表所示.
①请根据第2组和第5组数据计算得到该苹果电池的电动势E=1.00V;内电阻r=1.06kΩ.(结果保留两位小数).
②除苹果电池、电压表、电流表、电键、导线若干外,可供选择的实验器材有:滑动变阻器R1(阻值0~10Ω);电阻箱R2(阻值0~9999.9Ω),该电路中可变电阻应选择R2(选填R1或R2)
②请选择合适器材用铅笔划线代替导线将图乙中实物连接完整.

(1)实验前,甲同学利用调好的多用电表欧姆“×100”档来粗测该苹果电池的内阻.测量结果如图甲所示.他这样做是否正确?若正确,请读出其内阻值;若不正确,请说明理由.不正确 水果电池为电源,欧姆表不能电源的内阻.
(2)乙同学设计好测量电路,选择合适的器材,得到苹果电池两端的电压U和流过它的电流I的几组数据,如下表所示.
| 数据序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| U/V | 0.85 | 0.81 | 0.75 | 0.68 | 0.62 | 0.54 |
| I/mA | 0.14 | 0.18 | 0.24 | 0.32 | 0.36 | 0.48 |
②除苹果电池、电压表、电流表、电键、导线若干外,可供选择的实验器材有:滑动变阻器R1(阻值0~10Ω);电阻箱R2(阻值0~9999.9Ω),该电路中可变电阻应选择R2(选填R1或R2)
②请选择合适器材用铅笔划线代替导线将图乙中实物连接完整.
9.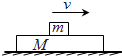 如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )
如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )
 如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )
如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )| A. | f1=μ1 Mg f2=μ1 mg | B. | f1=μ1(M+m)g f2=μ1 mg | ||
| C. | f1=μ1Mg f2=μ2mg | D. | f1=μ1(M+m)g f2=μ2 mg |
16.丹麦物理学家奥斯特在1820年发现了电流的磁效应,奥斯特在实验中,将直导线沿南北方向水平放置,指针靠近直导线,下列结论正确的是( )
| A. | 把小磁针放在导线的延长线上,通电后小磁针会转动 | |
| B. | 把小磁针平行地放在导线的下方,通电后小磁针不会立即发生转动 | |
| C. | 把小磁针平行地放在导线的下方,给导线通以恒定电流,然后逐渐增大导线与小磁针之间的距离,小磁针转动的角度(与通电前相比)会逐渐增大 | |
| D. | 把黄铜针(用黄铜制成的指针)平行地放在导线的下方,通电后黄铜针一定会转动 |
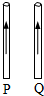
13.如图,两方向相同的直线电流P、Q,若Ip>Iq,P、Q受到安培力大小分别 为F1和F2,则P和Q( )

| A. | 相互吸引.F1>F2 | B. | 相互排斥.F1>F2 | C. | 相互排斥.F1=F2 | D. | 相互吸引.F1=F2 |
14.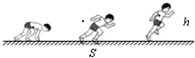 某运动员参加百米赛跑,他采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离S内,重心升高量为h,获得的速度为v,阻力做功为W阻,则在此过程中( )
某运动员参加百米赛跑,他采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离S内,重心升高量为h,获得的速度为v,阻力做功为W阻,则在此过程中( )
 某运动员参加百米赛跑,他采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离S内,重心升高量为h,获得的速度为v,阻力做功为W阻,则在此过程中( )
某运动员参加百米赛跑,他采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图所示,假设质量为m的运动员,在起跑时前进的距离S内,重心升高量为h,获得的速度为v,阻力做功为W阻,则在此过程中( )| A. | 运动员的机械能增加了$\frac{1}{2}$mv2 | |
| B. | 运动员的机械能增加了$\frac{1}{2}$mv2+mgh | |
| C. | 运动员的重力做功为W重=mgh | |
| D. | 运动员自身做功W人=$\frac{1}{2}$mv2+mgh-W阻 |