Question

【题目】在高为1m的水平桌面上有A，B两个小物体，其中B放在桌子的右边缘，A放在弹簧的右端O处但不拴接（弹簧的左端固定在桌上，处于自然状态），LOB=2m，现用A将弹簧压缩后静止释放，在以后运动的过程中A与B发生弹性碰撞，B的落地点到桌子边缘的水平距离为2m，A，B的质量分别为m，M，m=lkg，M=2kg，（水平面上O点的左侧光滑，右侧的动摩擦因数为0.5）求：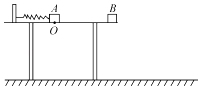

（1）A最终静止在什么位置？
（2）弹簧的最大弹性势能EP．

Answer 1

【答案】
（1）解：设A离开弹簧后的速率为v0，与B碰前的速率为v，碰后的速度为v1，B的速度为v2，

A、B相碰时，取向右为正方向，由动量守恒定律得：

mv=mv1+Mv2，

mv2= mv12+ Mv22，

解得：v1=﹣ v，v2= v

B碰后做平抛运动，x=v2t=2m，h= gt2

解得：v2=2 m/s，故 v=3 m/s，v1=﹣ m/s

A碰后做匀减速运动，vA=0时其位移为xA，

由动能定理得：﹣μmgxA=0﹣

解得 xA=0.5m，即A停在距桌子右边缘0.5m处

答：A最终距桌子右边缘0.5m处．

（2）A从O点到B处做匀减速运动，由动能定理得

﹣μmgLOB= ﹣

得 v0= = = m/s

A被弹开的过程，A和弹簧组成的系统机械能守恒，则

EP= mv02= ×1×65J=32.5J

答：弹簧的最大弹性势能是32.5J．

【解析】（1）两物块相碰的过程满足动量守恒和能量守恒，列方程组求出两物块的速度，离开桌面后B物体做平抛运动，A物体做匀减速运动结合动能定理和平抛运动的规律，列方程组求解即可.
（2）A物块被弹开的过程，机械能守恒，利用动能定理求出物块的初速度，再利用机械能守恒，求弹簧的最大弹性势能。