题目内容
 如图,水平光滑绝缘轨道MN的左端有一固定绝缘挡板,轨道所在空间存在水平向左、E=4×102N/C的匀强电场.一个质量m=0.2kg、带电荷量q=5.0×10-5C的滑块(可视为质点),从轨道上与挡板相距x1=0.2m的P点由静止释放,滑块在电场力作用下向左做匀加速直线运动.当滑块与挡板碰撞后滑块沿轨道向右做匀减速直线运动,运动到与挡板相距x2=0.1m的Q点,滑块第一次速度减为零.若滑块在运动过程中,电荷量始终保持不变,求:
如图,水平光滑绝缘轨道MN的左端有一固定绝缘挡板,轨道所在空间存在水平向左、E=4×102N/C的匀强电场.一个质量m=0.2kg、带电荷量q=5.0×10-5C的滑块(可视为质点),从轨道上与挡板相距x1=0.2m的P点由静止释放,滑块在电场力作用下向左做匀加速直线运动.当滑块与挡板碰撞后滑块沿轨道向右做匀减速直线运动,运动到与挡板相距x2=0.1m的Q点,滑块第一次速度减为零.若滑块在运动过程中,电荷量始终保持不变,求:(1)滑块由静止释放时的加速度大小a;
(2)滑块从P点第一次达到挡板时的速度大小v;
(3)滑块与挡板第一次碰撞的过程中损失的机械能△E.
分析:(1)光滑绝缘的轨道没有摩擦力,滑块水平方向只受电场力作用,根据牛顿第二定律可以求出加速度的大小;
(2)对向左加速过程运用动能定理列式求解即可;
(3)根据功能关系,与挡板碰撞过程中损失的机械能等于电场力作P到Q对滑块所做的功.
(2)对向左加速过程运用动能定理列式求解即可;
(3)根据功能关系,与挡板碰撞过程中损失的机械能等于电场力作P到Q对滑块所做的功.
解答:解:(1)设滑块沿轨道向左做匀加速运动的加速度为a,根据牛顿第二定律有:
qE=ma
代入数据得:a=
=
=0.1m/s2.
(2)滑块从P点运动到挡板处的过程中,由动能定理有:
qEx1=
mv2
代入数据有:v=
=
=0.2m/s
(3)滑块第一次与挡板碰撞过程中损失的机械能等于滑块由P点运动到Q点过程中电场力所做的功,即:
△E=qE(x1-x2)=2×10-3J.
答:(1)滑块由静止释放时的加速度大小a为0.1m/s2;(2)滑块从P点第一次达到挡板时的速度大小为0.2m/s;
(3)滑块与挡板第一次碰撞的过程中损失的机械能△E为2×10-3J.
qE=ma
代入数据得:a=
| qE |
| m |
| 5×10-5×4×102 |
| 0.2 |
(2)滑块从P点运动到挡板处的过程中,由动能定理有:
qEx1=
| 1 |
| 2 |
代入数据有:v=
|
|
(3)滑块第一次与挡板碰撞过程中损失的机械能等于滑块由P点运动到Q点过程中电场力所做的功,即:
△E=qE(x1-x2)=2×10-3J.
答:(1)滑块由静止释放时的加速度大小a为0.1m/s2;(2)滑块从P点第一次达到挡板时的速度大小为0.2m/s;
(3)滑块与挡板第一次碰撞的过程中损失的机械能△E为2×10-3J.
点评:本题运用功能关系求解分析滑块与挡板碰撞所损失的机械能△E,也可以根据动能定理分过程求解.

练习册系列答案
相关题目
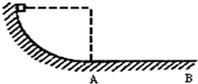 如图所示,质量为0.2Kg的物体带电量为1×10-3C,从半径为0.45m的光滑的1/4圆弧的绝缘滑轨上端由静止下滑到底端,然后继续沿水平面滑动.
如图所示,质量为0.2Kg的物体带电量为1×10-3C,从半径为0.45m的光滑的1/4圆弧的绝缘滑轨上端由静止下滑到底端,然后继续沿水平面滑动.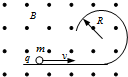 如图,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B.有一个质量m,带正电量为q的小球在水平轨道上向右运动.恰好能通过最高点,下列正确的是( )
如图,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B.有一个质量m,带正电量为q的小球在水平轨道上向右运动.恰好能通过最高点,下列正确的是( )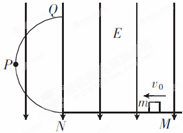 (2011?安徽模拟)如图所示,在E=1×103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,与水平轨道间的动摩擦因数μ=0.15,位于N点右侧1.5m处,取g=10m/s2,求:
(2011?安徽模拟)如图所示,在E=1×103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,与水平轨道间的动摩擦因数μ=0.15,位于N点右侧1.5m处,取g=10m/s2,求: 如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,重力加速度g=10m/s2.试求:
如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,重力加速度g=10m/s2.试求: (2007?湖北模拟)如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,则下列说法正确的是( )
(2007?湖北模拟)如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,则下列说法正确的是( )