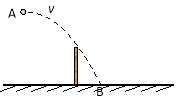Question

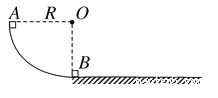
【题目】如图所示，半径R=1.25m的竖直平面内的光滑四分之一圆弧轨道下端与水平桌面相切。质量为m1=0.2kg小滑块A和质量为m2=0.6kg的小滑块B分别静止在圆弧轨道的最高点和最低点。现将A无初速度释放，A与B碰撞后A沿圆弧轨道上升的最大高度h=0.05m。取重力加速度g=10m/s2。求：

(1)碰撞前瞬间A的速率v0；

(2)碰撞过程系统损失的机械能。

Answer 1

【答案】(1)；(2)

【解析】

(1)对小滑块A沿圆弧轨道的下滑过程，根据机械能守恒

解得

(2)碰撞后，对A上升过程，由机械能守恒定律有

解得碰撞后A的速度大小

A的速度方向向左。规定水平向右为正方向，由动量守恒定律有

m1v0=-m1v1＋m2v2

解得碰撞后瞬间B的速度大小为

v2=2m/s

B的速度方向向右。碰撞过程系统损失的机械能