题目内容
如图所示,左端带挡板的长为2L的木板B静止在水平面上,一质量为m(可视为质点)的物块A停在长木板的左端,挡板和物块间用长为L的轻绳连接,木板B质量为2m,A与B之间、B与水平面之间的动摩擦因数均为μ.现给物块A持续施加一大小恒为F=2μmg的水平拉力,使A由静止开始在B上向右运动,当绳拉直后立即绷断,且绷断时B的速度小于A的速度(绳绷断后力F仍未撤除),其后木板B滑行了 L停止.求:
L停止.求:(1)从刚开始运动到绳刚被拉直过程中物块A的加速度aA及经历的时间tA;
(2)绳绷断后瞬间,物块A的速度vA和木板B的速度vB;
(3)绳绷断时至物块A滑离木板B,物块A的对地位移.

【答案】分析:(1)以木块A为研究对象,受力分析,由牛顿第二定律求出加速度,然后由匀变速运动的位移公式求出A的运动时间.
(2)由匀变速运动的速度公式求出绳绷直时A的速度,绳子绷断后,B做匀减速运动,由牛顿第二定律求出B的加速度,由匀变速运动的速度位移公式求出B的初速度,绳子绷断的瞬间AB组成的系统动量守恒,由动量守恒定律列方程,然后求出绳子绷断时A的速度.
(3)根据AB间的相对运动情况,分析绳子绷断后A与B的运动情况,然后求出A相对于地的位移.
解答:解:(1)绳绷直前木板B一直静止,木板B的加速度aB=0;
在拉力作用下物块A在木板上向右做初速度为零的匀加速直线运动,
由牛顿第二定律得:物块A的加速度aA= =μg;
=μg;
由匀变速运动的位移公式得:L= aAtA2,解得:tA=
aAtA2,解得:tA=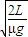 ;
;
(2)绳刚绷直时物块A的速度为v=aAtA= ,
,
绳子绷断后,因木板B速度小于物块A速度,A对B的滑动摩擦力向μmg向右,
地面对B的滑动摩擦力μ(m+2m)=3μmg向左,由牛顿第二定律得:
木板B加速度为aB′=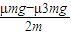 =-μg,负号表示加速度方向向左,
=-μg,负号表示加速度方向向左,
木板B匀减速前进 后停止,由0-vB2=2aB′?
后停止,由0-vB2=2aB′?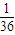 L,解得:vB=
L,解得:vB=
 ;
;
绳绷断前后瞬间AB组成的系统动量守恒:
设绳绷断后物块A速度为vA,木板B速度为vB,
由动量守恒定律得:mv=mvA+2mvB,解得:vA=
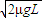 ;
;
(3)绳绷断后,木板B滑行了 <L,木板B停止运动时,A仍然在木板上,
<L,木板B停止运动时,A仍然在木板上,
B停止运动后,物块A还需相对木板B滑行L才能滑离木板B,物块A直接在木板上对地匀加速滑出.
B向右滑动时,A随B一起向右滑动了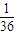 L,绷断后物块A的对地位移为:sA′=
L,绷断后物块A的对地位移为:sA′= +L=
+L= L;
L;
答:(1)从刚开始运动到绳刚被拉直过程中物块A的加速度aA=μg,经历的时间tA=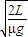 ;
;
(2)绳绷断后瞬间,物块A的速度vA=
 ,木板B的速度vB=
,木板B的速度vB=
 ;
;
(3)绳绷断时至物块A滑离木板B,物块A的对地位移为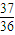 L.
L.
点评:本题是一道综合题,难度较大;分析清楚AB的运动过程是正确解题的关键,对AB正确受力分析、应用运动学公式、牛顿第二定律、动量守恒定律即可正确解题.
(2)由匀变速运动的速度公式求出绳绷直时A的速度,绳子绷断后,B做匀减速运动,由牛顿第二定律求出B的加速度,由匀变速运动的速度位移公式求出B的初速度,绳子绷断的瞬间AB组成的系统动量守恒,由动量守恒定律列方程,然后求出绳子绷断时A的速度.
(3)根据AB间的相对运动情况,分析绳子绷断后A与B的运动情况,然后求出A相对于地的位移.
解答:解:(1)绳绷直前木板B一直静止,木板B的加速度aB=0;
在拉力作用下物块A在木板上向右做初速度为零的匀加速直线运动,
由牛顿第二定律得:物块A的加速度aA=
 =μg;
=μg;由匀变速运动的位移公式得:L=
 aAtA2,解得:tA=
aAtA2,解得:tA=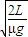 ;
;(2)绳刚绷直时物块A的速度为v=aAtA=
 ,
,绳子绷断后,因木板B速度小于物块A速度,A对B的滑动摩擦力向μmg向右,
地面对B的滑动摩擦力μ(m+2m)=3μmg向左,由牛顿第二定律得:
木板B加速度为aB′=
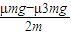 =-μg,负号表示加速度方向向左,
=-μg,负号表示加速度方向向左,木板B匀减速前进
 后停止,由0-vB2=2aB′?
后停止,由0-vB2=2aB′?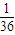 L,解得:vB=
L,解得:vB=
 ;
;绳绷断前后瞬间AB组成的系统动量守恒:
设绳绷断后物块A速度为vA,木板B速度为vB,
由动量守恒定律得:mv=mvA+2mvB,解得:vA=

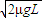 ;
;(3)绳绷断后,木板B滑行了
 <L,木板B停止运动时,A仍然在木板上,
<L,木板B停止运动时,A仍然在木板上,B停止运动后,物块A还需相对木板B滑行L才能滑离木板B,物块A直接在木板上对地匀加速滑出.
B向右滑动时,A随B一起向右滑动了
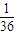 L,绷断后物块A的对地位移为:sA′=
L,绷断后物块A的对地位移为:sA′= +L=
+L= L;
L;答:(1)从刚开始运动到绳刚被拉直过程中物块A的加速度aA=μg,经历的时间tA=
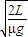 ;
;(2)绳绷断后瞬间,物块A的速度vA=

 ,木板B的速度vB=
,木板B的速度vB=
 ;
;(3)绳绷断时至物块A滑离木板B,物块A的对地位移为
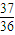 L.
L.点评:本题是一道综合题,难度较大;分析清楚AB的运动过程是正确解题的关键,对AB正确受力分析、应用运动学公式、牛顿第二定律、动量守恒定律即可正确解题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
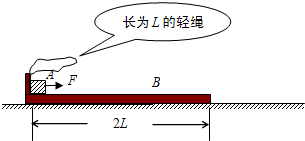 如图所示,左端带挡板的长为2L的木板B静止在水平面上,一质量为m(可视为质点)的物块A停在长木板的左端,挡板和物块间用长为L的轻绳连接,木板B质量为2m,A与B之间、B与水平面之间的动摩擦因数均为μ.现给物块A持续施加一大小恒为F=2μmg的水平拉力,使A由静止开始在B上向右运动,当绳拉直后立即绷断,且绷断时B的速度小于A的速度(绳绷断后力F仍未撤除),其后木板B滑行了
如图所示,左端带挡板的长为2L的木板B静止在水平面上,一质量为m(可视为质点)的物块A停在长木板的左端,挡板和物块间用长为L的轻绳连接,木板B质量为2m,A与B之间、B与水平面之间的动摩擦因数均为μ.现给物块A持续施加一大小恒为F=2μmg的水平拉力,使A由静止开始在B上向右运动,当绳拉直后立即绷断,且绷断时B的速度小于A的速度(绳绷断后力F仍未撤除),其后木板B滑行了

