题目内容
如图所示,左端带挡板的长为2L的木板B静止在水平面上,一质量为m(可视为质点)的物块A停在长木板的左端,挡板和物块间用长为L的轻绳连接,木板B质量为2m,A与B之间、B与水平面之间的动摩擦因数均为μ.现给物块A持续施加一大小恒为F = 2μmg的水平拉力,使A由静止开始在B上向右运动,当绳拉直后立即绷断,且绷断时B的速度小于A的速度(绳绷断后力F仍未撤除),其后木板B滑行了L停止.求:
(1)从刚开始运动到绳刚被拉直过程中物块A的加速度aA及经历的时间tA;
(2)绳绷断后瞬间,物块A的速度vA和木板B的速度vB;
(3)绳绷断时至物块A滑离木板B,物块A的对地位移.

解答:
(1)可分析:绳绷直前木板B一直静止
即:木板B的加速度
在拉力作用下物块A在木板上向右做匀加速直线运动
则物块A的加速度为  (2分)
(2分)
所用时间 由 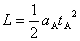 得
得
 (2分)
(2分)
(2)绳刚绷直时物块A的速度为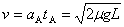 (1分)
(1分)
绳绷断前后瞬间系统动量守恒:
设绳绷断后物块A速度为 ,木板B速度为
,木板B速度为
则有
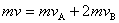 (2分)
(2分)
之后:因木板B速度小于物块A速度,
则木板B加速度为  (负号表示方向水平向左)
(负号表示方向水平向左)
木板B匀减速前进 后停止:由
后停止:由
可得
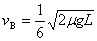 (2分)
(2分)
代入动量守恒方程得  (2分)
(2分)
(3)(判断A停止运动后B才掉下来)绳绷断后,木板B滑行了 停止,
物块A还需相对木板B滑行L才滑离,
停止,
物块A还需相对木板B滑行L才滑离,
物块A直接在木板上对地匀加速滑出.故绷断后物块A的对地位移为: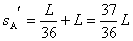 (3分)
(3分)

 备战中考寒假系列答案
备战中考寒假系列答案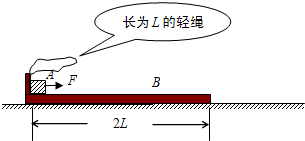 如图所示,左端带挡板的长为2L的木板B静止在水平面上,一质量为m(可视为质点)的物块A停在长木板的左端,挡板和物块间用长为L的轻绳连接,木板B质量为2m,A与B之间、B与水平面之间的动摩擦因数均为μ.现给物块A持续施加一大小恒为F=2μmg的水平拉力,使A由静止开始在B上向右运动,当绳拉直后立即绷断,且绷断时B的速度小于A的速度(绳绷断后力F仍未撤除),其后木板B滑行了
如图所示,左端带挡板的长为2L的木板B静止在水平面上,一质量为m(可视为质点)的物块A停在长木板的左端,挡板和物块间用长为L的轻绳连接,木板B质量为2m,A与B之间、B与水平面之间的动摩擦因数均为μ.现给物块A持续施加一大小恒为F=2μmg的水平拉力,使A由静止开始在B上向右运动,当绳拉直后立即绷断,且绷断时B的速度小于A的速度(绳绷断后力F仍未撤除),其后木板B滑行了

 L停止.求:
L停止.求: