题目内容
如图所示，质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射入两平行板间的匀强电场中，P从两极板正中央射入，Q从下极板边缘处射入，它们最后打在同一点（重力不计），则从开始射入到打到上板的过程中（ ）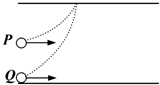
| A．它们运动的时间tQ>tP |
| B．它们运动的加速度aQ<aP |
| C．它们所带的电荷量之比qP∶qQ=1∶2 |
| D．它们的动能增加量之比ΔEkP∶ΔEkQ=1∶2 |
C
解析试题分析：带电粒子在垂直电场方向不受力，做匀速直线运动，位移相等，根据
，得到运动时间相等；平行电场方向受到电场力，做初速度为零的匀加速直线运动，根据位移时间关系公式
，得
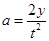，由于两带电粒子平行电场方向分位移之比为1：2，因此
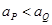；根据牛顿第二定律，有
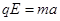，可得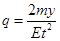
，则它们所带的电荷量之比
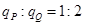；根据动能定理，有
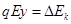，而，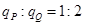
，则动能增加量之比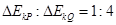
，所以正确选项为C。
考点：本题考查了带电粒子在匀强电场中的运动和动能定理的应用。
智慧小复习系列答案把导体匀速拉上斜面，如图所示，则下列说法正确的是（不计棒和导轨的电阻，且接触面光滑，匀强磁场磁感应强度B垂直框面向上）（ ）
| A．拉力做的功等于棒的机械能的增量 |
| B．拉力对棒做的功等于棒的动能的增量 |
| C．拉力与棒受到的磁场力的合力为零 |
| D．拉力对棒做的功与棒克服重力做的功之差等于回路中产生电能 |
如图，两个半径均为R的1/4光滑圆弧对接于O点，有物体从上面圆弧的某点C以上任意位置由静止下滑（C点未标出），都能从O点平抛出去，则（ ）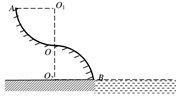
| A．∠CO1O=60° |
| B．∠CO1O=45° |
| C．落地点距O2最远为2R |
| D．落地点距O2最近为R |
如图所示，甲、乙两种粗糙面不同的传送带，倾斜放于水平地面，与水平面的夹角相同，以同样恒定速率v向上运动。现将一质量为m的小物体（视为质点）轻轻放在A处，小物体在甲传送带上到达B处时恰好达到速率v；在乙上到达离B竖直高度为h的C处时达到速率v，已知B处离地面高度皆为H。则在物体从A到B过程中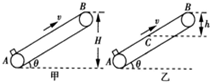
| A．小物块在两种传送带上具有的加速度相同 |
| B．将小物体传送到B处，两种传送带消耗的电能相等 |
| C．两种传送带对小物体做功相等 |
| D．将小物体传送到B处，两种系统产生的热量相等 |
将三个木板1、2、3固定在墙角，木板与墙壁和地面构成了三个不同的三角形，如图所示，其中1与2底边相同，2和3高度相同。现将一个可以视为质点的物块分别从三个木板的顶端由静止释放，并沿木板下滑到底端，物块与木板之间的动摩擦因数μ均相同。在这三个过程中，下列说法正确的是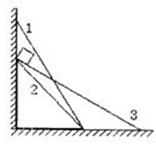 
| A．物块沿着3下滑到底端的过程中，产生的热量是最多的 |
| B．沿着1下滑到底端时，物块的速度最大 |
| C．物块沿着1和2下滑到底端的过程中，产生的热量是一样多的 |
| D．沿着1和2下滑到底端时，物块的速度不同；沿着2和3下滑到底端时，物块的速度相同 |
如图所示，空间有一水平方向的匀强电场，初速度为v0的带电小球从A点射入电场，在竖直平面内沿直线从A运动到B，在此过程中粒子的( )
| A．动能和电势能都减少，重力势能增加 |
| B．动能减少，重力势能和电势能都增加 |
| C．动能和重力势能都增加，电势能减少 |
| D．动能不变，重力势能增加，电势能减少 |
轻质弹簧右端固定在墙上，左端与一质量m=0.5kg的物块相连，如图甲所示。弹簧处于原长状态，物块静止且与水平面间的动摩擦因数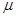
=0.2。以物块所在处为原点，水平向右为正方向建立x轴。现对物块施加水平向右的外力F，F随x轴坐标变化的情况如图乙所示。物块运动至x=0.4m处时速度为零。则此时弹簧的弹性势能为(g=10m/S2)
| A．3.1 J | B．3.5 J | C．1.8 J | D．2.0J |
如图所示，质量为m的物体用细绳拴住放在水平粗糙传送带上，物体距传送带左端距离为L，稳定时绳与水平方向的夹角为θ，当传送带分别以速度v1、v2做逆时针转动时（v1<v2），绳的拉力大小分别为F1、F2；若剪断细绳后，物体到达左端经历的时间分别为t1、t2，则下列说法正确的是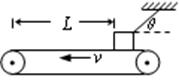
| A．F1<F2 |
| B．F1=F2 |
| C．t1一定大于t2 |
| D．t1可能等于t2 |