题目内容
16.如图1所示,在2010上海世博会上,拉脱维亚馆的风洞飞行表演,令参观者大开眼界,最吸引眼球的就是正中心那个高为H=10m,直径D=4m的透明“垂直风洞”.风洞是人工产生和控制的气流,以模拟飞行器或物体周围气体的流动.在风力作用的正对面积不变时,风力F=0.06v2(v为风速).在本次风洞飞行上升表演中,表演者的质量m=60kg,为提高表演的观赏性,控制风速v与表演者上升的高度h间的关系如图2所示.g=10m/s2.求:
(1)设想:表演者开始静卧于h=0处,再打开气流,请描述表演者从最低点到最高点的运动状态;先做加速度减小的加速运动,后做加速度增加的减速运动
(2)表演者上升达最大速度时的高度h1;
(3)表演者上升的最大高度h2;
(4)为防止停电停风事故,风洞备有应急电源,若在本次表演中表演者在最大高度h2时突然停电,为保证表演者的人身安全,则留给风洞自动接通应急电源滞后的最长时间tm.(设接通应急电源后风洞一直以最大风速运行)
分析 (1)表演者开始静卧于h=0处,再打开气流,受到向上的风力和重力作用,向上做加速运动.根据图象,分析风力的变化,由牛顿第二定律确定加速度的变化.
(2)表演者在上升过程中当风力与重力平衡时,速度达到最大值.由图2得出v与h的关系式,代入风力F=0.06v2,得到F与h的关系,由平衡条件求出高度h1.
(3)根据F与h的关系求出表演者上升过程中风力做的功,再由动能定理求出表演者上升的最大高度h2.
(4)应急电源接通前,表演者先做自由落体运动;当应急电源接通后,做匀减速运动,恰好落到风洞底部时速度为零.根据牛顿第二定律和位移公式结合求出tm.
解答 解:(1)表演者开始静卧于h=0处,再打开气流,受到向上的风力和重力作用,先向上做加速运动.由图知,v2(v为风速)减小,风力F=0.06v2,则风力减小,故表演者的加速度加速度减小.当风力小于重力时,表演者做减速运动,加速度增大,故先向上做加速度减小的变加速运动,后向上做加速度增大的减速运动,到达最高点时速度为零.
(2)由图2可知v2=1.2×104-500h
则风力 F=0.06v2=7.2×102-30h
当表演者在上升过程中的最大速度vm时有F=mg
代入数据得h1=4m.
(2)对表演者,由动能定理得 WF-mgh2=0
因WF与h成线性关系,风力做功${W}_{F}=\frac{{F}_{0}+{F}_{k2}}{2}{h}_{2}$
由F=0.06v2=7.2×102-30h得
h=0时,F0=7.2×102N
h=h2时,Fh2=7.2×102-30h2,m=60kg
代入数据化解得h2=8m
(3)当应急电源接通后以风洞以最大风速运行时滞后时间最长,
表演者减速的加速度为$a=\frac{{F}_{m}-mg}{m}$=2m/s2
表演者从最高处到落地过程有
H=$\frac{1}{2}g{t}_{m}^{2}+\frac{(g{t}_{m})^{2}}{2a}$
代入数据化简得:
${t}_{m}=\frac{2\sqrt{15}}{15}s$≈0.52s.
答:(1)设想:表演者开始静卧于h=0处,再打开气流,表演者先向上做加速度减小的变加速运动,后向上做加速度增大的减速运动,到达最高点时速度为零.
(2)表演者上升达最大速度时的高度h1是4m.
(3)表演者上升的最大高度h2是8m.
(4)留给风洞自动接通应急电源滞后的最长时间tm是0.52s.
点评 本题根据图象写出解析式,充分利用图象的信息是本题的关键.当力与位移成线性变化时可用力的平均值与位移乘积求变化做功.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 现有P、Q两个小球,被长度不等的细线悬挂在同一点,并在同一水平面内做匀速圆运动,如图所示.则( )
现有P、Q两个小球,被长度不等的细线悬挂在同一点,并在同一水平面内做匀速圆运动,如图所示.则( )| A. | 两小球周期相同 | |
| B. | P球线速度的值大于Q球线速度的值 | |
| C. | P球向心加速度的值大于Q球向心加速度的值 | |
| D. | P球角速度的值大于Q球角速度的值 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{24}$ |
 火箭点火后竖直上升的过程可简化为下列几个过程:
火箭点火后竖直上升的过程可简化为下列几个过程:(1)点火后匀加速上升
(2)熄火后继续上升
(3)上升到最高点后下落.
其v-t图象如图,下列说法正确的是 ( )
| A. | 在40秒末火箭已达到上升的最大速度 | |
| B. | 火箭达到最高点的时刻是40秒末 | |
| C. | 火箭落地的时刻是120秒末 | |
| D. | 熄火后火箭的加速度为零 |
 如图所示,木块A放在水平的长木板上,长木板放在光滑的水平桌面上.木块与水平的弹簧秤相连,弹簧秤的右端固定.若用水平向左的恒力拉动长木板以速度v匀速运动,弹簧秤的示数为FT.则( )
如图所示,木块A放在水平的长木板上,长木板放在光滑的水平桌面上.木块与水平的弹簧秤相连,弹簧秤的右端固定.若用水平向左的恒力拉动长木板以速度v匀速运动,弹簧秤的示数为FT.则( )| A. | 木块A受到的静摩擦力等于FT | |
| B. | 木块A受到的滑动摩擦力等于FT | |
| C. | 若用恒力以2v的速度匀速向左拉动长木板,弹簧秤的示数为FT | |
| D. | 若用恒力以2v的速度匀速向左拉动长木板,弹簧秤的示数为2FT |
 如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2.若将滑块从位置A由静止释放,当落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则这时物块的速度大小v1等于( )
如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为m1和m2,且m1<m2.若将滑块从位置A由静止释放,当落到位置B时,滑块的速度为v2,且与滑块牵连的绳子与竖直方向的夹角为θ,则这时物块的速度大小v1等于( )| A. | v2sinθ | B. | $\frac{{v}_{2}}{sinθ}$ | C. | v2cosθ | D. | $\frac{{v}_{2}}{cosθ}$ |
| A. | 作用力和反作用力总是同时消失 | |
| B. | 作用力与反作用力互相平衡 | |
| C. | 弹力的反作用力亦可能是摩擦力 | |
| D. | 当相互作用的物体都处于平衡状态时,它们之间的作用与反作用大小才相等 |
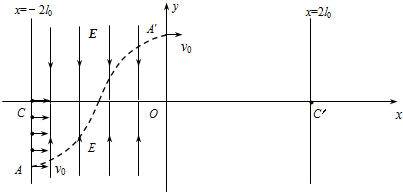 如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用.
如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图.不计粒子的重力及它们间的相互作用. 如图所示,在直线MN下方有一个水平向右的匀强电场,在直线上方没有任何电场,O为MN上一点,在O点悬挂两根长度均为L的轻绳,轻绳下端各悬挂一个质量均为m、带电荷量分别为-q、+q(电荷量的数值相等)的小球A和B.两个小球之间用第三根长度同为L的轻绳拴住.(不计两个小球之间的库仑力作用)
如图所示,在直线MN下方有一个水平向右的匀强电场,在直线上方没有任何电场,O为MN上一点,在O点悬挂两根长度均为L的轻绳,轻绳下端各悬挂一个质量均为m、带电荷量分别为-q、+q(电荷量的数值相等)的小球A和B.两个小球之间用第三根长度同为L的轻绳拴住.(不计两个小球之间的库仑力作用)