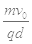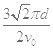题目内容
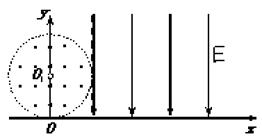
（17分）如图所示，真空中有以O1为圆心，r为半径的圆形匀强磁场区域，坐标原点O为圆形磁场边界上的一点。磁场的磁感应强度大小为B，方向垂直于纸面向外。x=r的虚线右侧足够大的范围内有方向竖直向下、大小为E的匀强电场。从O点在纸面内向各个不同方向发射速率相同的质子，设质子在磁场中的偏转半径也为r，已知质子的电荷量为e，质量为m。求：
(1)质子射入磁场时的速度大小；
(2)速度方向沿y轴正方向射入磁场的质子到达x轴所需的时间；
(3)速度方向与y轴正方向成37°角且与x轴正方向成127°角射入磁场的质子到达x轴时的位置坐标。(已知sin37°＝0.6，cos37°="0.8)"
(1)质子射入磁场时的速度大小；
(2)速度方向沿y轴正方向射入磁场的质子到达x轴所需的时间；
(3)速度方向与y轴正方向成37°角且与x轴正方向成127°角射入磁场的质子到达x轴时的位置坐标。(已知sin37°＝0.6，cos37°="0.8)"
（1）v=eBr/m（2 
（3）（
,0）
（3）（,0）试题分析：（1)设质子射磁场时的速度为v。质子射入磁场后做匀速圆周运动，有evB=mv2/r （2分）
所以v="eBr/m" （1分）
(2)如图，质子沿y轴正方向射入，在磁场中以O2为圆心转过1/4圆弧后从A点垂直于电场方向进入电场。在磁场中的运动周期为T="2πm/(eB)" （1分）
所以质子在磁场中的运动时间 t1="T/4=πm/(2eB)" （1分）
质子进入电场后做类平抛运动，其侧移距离y=at22/2=r（1分）
质子在电场中的加速度a=eE/m（1分）
所以质子在电场中的运动时间t2=
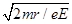（1分）故质子到达x轴所需的时间t=t1+t2=πm/(2eB)+
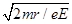（1分）(3)质子射入磁场后，在磁场中以O3为圆心做匀速圆周运动，从P点射出磁场，如图所示，OO1PO3是边长为r的菱形，PO3平行于y轴，质子射出磁场后速度方向与x轴平行。
P点距x轴的距离h=r+rcos53°（3分）
质子垂直于电场方向进入电场做类平抛运动，到达x轴上的Q点。竖直方向的位移h=eEt2/2m （2分）
水平方向的位移s=vt（1分）
解得：
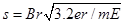（1分）所以Q点的坐标为（
,0）（1分）
练习册系列答案
相关题目
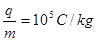，OP间距离为l＝0.3m。全过程不计粒子所受的重力，求：
＝4×10－10 kg/C的带正电粒子从x轴上的A点以初速度v0＝2×107 m/s垂直x轴射入电场，OA＝0.2 m，不计重力．求：
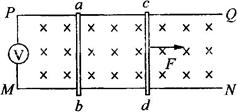
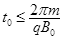且为未知量。求：
