题目内容
12.如图所示,x轴上方有竖直向下的匀强电场,x轴下方有垂直纸面向外的匀强磁场.矩形OACD的边长分别为h和2h一个带正电的粒子,质量为m电荷量为q,以平行于x轴的某一初速度从A点射出,经t0时间粒子从D点进入磁场,再经过一段时间后粒子又一次经过A点(重力忽略不计).求: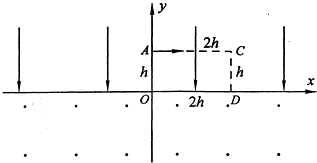
(1)电场强度大小E;
(2)磁感应强度大小B;
(3)若仅改变粒子初速度的大小,求粒子以最短时间由A运动到C所需的初速度大小vx.
分析 (1)带电粒子进入电场中做类平抛运动,根据水平位移和初速度求出运动的时间,根据牛顿第二定律和位移时间公式求出电场强度的大小.
(2)根据粒子的速度方向,结合半径公式和几何关系求出磁感应强度的大小.
(3)粒子出磁场后运动到离x轴最大距离处时竖直速度为零,看作反向的平抛运动,根据周期公式求出粒子在磁场中运动的时间,以及粒子在电场中做类平抛运动的时间,从而得出总时间.
解答 解:(1)带电粒子在电场中做类平抛运动,由h=$\frac{1}{2}a{t}_{0}^{2}$ ①
得 a=$\frac{2h}{{t}_{0}^{2}}$
又 qE=ma ②
可得 E=$\frac{ma}{q}$=$\frac{2mh}{q{t}_{0}^{2}}$ ③
(2)由vx=$\frac{2h}{{t}_{0}}$,vy=at0=$\frac{2h}{{t}_{0}^{2}}$•t0=vx,得
粒子进入磁场时的速度大小 v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\frac{2\sqrt{2}h}{{t}_{0}}$ ④
由R=$\frac{mv}{qB}$,得:$\frac{2\sqrt{2}mh}{qB{t}_{0}}$=2$\sqrt{2}$h ⑤
解得 B=$\frac{m}{q{t}_{0}}$ ⑥
(3)设速度大小为vx,运动轨迹与x轴交点处速度方向与x轴夹角为θ,
第一次与x轴相交时,vy=$\frac{2h}{{t}_{0}}$,合速度为v,交点坐标为 x2=vxt0.
sinθ=$\frac{{v}_{y}}{{v}_{0}}$ ⑦
又 R=$\frac{mv}{qB}$=vt0,⑧
得Rsinθ=vt0•$\frac{2h}{v{t}_{0}}$=2h,与初速度大小无关. ⑨
运动轨迹与x轴另一交点坐标为
x1=x2-2Rsinθ=vxt0-4h
根据对称性 x1=-h,x2=3h (10)
粒子以最短时间由A运动到C所需的初速度大小 vx=$\frac{3h}{{t}_{0}}$
答:
(1)电场强度大小E为$\frac{2mh}{q{t}_{0}^{2}}$;
(2)磁感应强度大小B为$\frac{m}{q{t}_{0}}$;
(3)若仅改变粒子初速度的大小,粒子以最短时间由A运动到C所需的初速度大小vx为$\frac{3h}{{t}_{0}}$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹,应用类平抛运动知识、牛顿第二定律、几何知识即可正确解题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案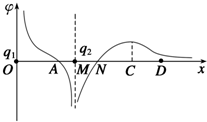 两电荷量分别为q1和q2的点电荷放在x轴上O、M两点,两电荷连线上各点电势φ随x变化的关系如图,其中A、N两点的电势为零,ND段中C点电势最高,则下列说法中正确的是( )
两电荷量分别为q1和q2的点电荷放在x轴上O、M两点,两电荷连线上各点电势φ随x变化的关系如图,其中A、N两点的电势为零,ND段中C点电势最高,则下列说法中正确的是( )| A. | q1带正电,q2带负电 | |
| B. | |q1|=|q2| | |
| C. | A点的电场强度大小为零 | |
| D. | 将一正点电荷从N点移到D点,电场力先做负功后做正功 |
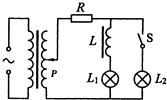 如图所示,理想变压器原线圈接有交流电源,副线圈上通过输电线接有灯泡Ll,L2和含有铁芯的线圈L,输电线等效电阻为R.开始时,开关S断开,滑片P处于图示位置,灯泡L1能发光.要使灯泡L1变亮,可以采取的办法是( )
如图所示,理想变压器原线圈接有交流电源,副线圈上通过输电线接有灯泡Ll,L2和含有铁芯的线圈L,输电线等效电阻为R.开始时,开关S断开,滑片P处于图示位置,灯泡L1能发光.要使灯泡L1变亮,可以采取的办法是( )| A. | 向上滑动P | B. | 闭合开关S | ||
| C. | 抽出线圈中的铁芯 | D. | 增大交流电源的频率 |
| A. | $\sqrt{\frac{n}{k}}$T | B. | $\sqrt{\frac{{n}^{2}}{k}}$T | C. | $\sqrt{\frac{{n}^{3}}{{k}^{2}}}$T | D. | $\sqrt{\frac{{n}^{3}}{k}}$T |
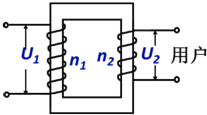 某型号变压器原副线圈匝数比为n1:n2=5:1,连接高压线变压后供电给市民,如图,则正确的是( )
某型号变压器原副线圈匝数比为n1:n2=5:1,连接高压线变压后供电给市民,如图,则正确的是( )| A. | 一般家庭电路的电压为U2=220$\sqrt{2}$V | |
| B. | 如果学校实验室也接入用户交流电,则打点计时器计时周期为0.02s | |
| C. | 变压器输入的交流电频率为250Hz | |
| D. | 用多用表测量U1约为1100V |
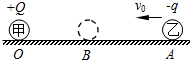 如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时静止.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为x,则( )
如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时静止.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为x,则( )| A. | OB间的距离为$\sqrt{\frac{kQq}{μmg}}$ | |
| B. | 从A到B的过程中,中间时刻的速度小于$\frac{{v}_{0}}{2}$ | |
| C. | 从A到B的过程中,产生的内能为$\frac{1}{2}$mv02 | |
| D. | 在点电荷甲形成的电场中,AB间电势差UAB=$\frac{m(v_0^2-2μgx)}{2q}$ |
 如图所示,在光滑的水平面上,质量为4m、长为L的木板右端紧靠竖直墙壁,与墙壁不粘连,质量为m的小滑块(可视为质点)以水平速度v0滑上木板左端,滑到木板右端时,速度恰好为零,现小滑块以水平速度v滑上木板左端,滑到木板右端时与竖直墙壁发生弹性碰撞,以原速率弹回,刚好能够滑到木板左端而不从木板上落下,求它们共同运动的速度.
如图所示,在光滑的水平面上,质量为4m、长为L的木板右端紧靠竖直墙壁,与墙壁不粘连,质量为m的小滑块(可视为质点)以水平速度v0滑上木板左端,滑到木板右端时,速度恰好为零,现小滑块以水平速度v滑上木板左端,滑到木板右端时与竖直墙壁发生弹性碰撞,以原速率弹回,刚好能够滑到木板左端而不从木板上落下,求它们共同运动的速度.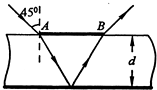 如图,足够长的平行玻璃砖厚度为d.有反光膜,顶面AB之间涂有长为$\frac{2\sqrt{3}}{3}$d的遮光物质一束光线以45°的入射角由A点入射,经底面反射后,恰能从B点射出.
如图,足够长的平行玻璃砖厚度为d.有反光膜,顶面AB之间涂有长为$\frac{2\sqrt{3}}{3}$d的遮光物质一束光线以45°的入射角由A点入射,经底面反射后,恰能从B点射出.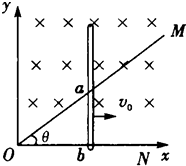 如图所示,顶角θ=45°的光滑金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r,导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触且没有脱离导轨.当t=0时,导体棒位于坐标原点o处,求:
如图所示,顶角θ=45°的光滑金属导轨 MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r,导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触且没有脱离导轨.当t=0时,导体棒位于坐标原点o处,求: