题目内容
19.用如图(a)所示的实验器材及电路测量金属丝的电阻率,实验的主要步骤如下.
①将P移到金属丝b端,电源调至E=4.00V,滑动变阻器的滑片滑至C端(填“C端”、“D端”或“中央”),闭合开关S,调节滑动变阻器使电流表读数为I0=0.50A.
②适当向a端滑动P,记录电流表读数I及电阻丝bP段的长度L;此时电阻丝bP段的阻值为R=$\frac{E}{I}$-$\frac{E}{{I}_{0}}$(用E、I和I0表示).
③重复步骤②,记录6组L和I值,画出$\frac{1}{I}$-L的关系图线如图(b);
④用螺旋测微器测量金属丝的直径如图(c),其示数为d=0.200mm;
⑤若用k表示$\frac{1}{I}$-L图线的斜率,则金属丝的电阻率为ρ=$\frac{kπE{d}^{2}}{4}$(用E、k、d和π表示).根据$\frac{1}{I}$-L图线,可算得ρ=6.3×10-7Ω•m (保留两位有效数字;π取3.14).
分析 ①滑动变阻器采用限流接法时,为保护电路滑片应置于阻值最大处.
②应用串联电路特点与欧姆定律可以求出电阻阻值.
④固定刻度与可动刻度示数之和是螺旋测微器的示数.
⑤求出图象的函数表达式,然后应用电阻定律求出电阻率表达式,然后代入数据求出电阻率.
解答 解:①为保护电路,闭合开关前滑片应置于C端.
②由欧姆定律可知,滑动变阻器接入电路的阻值:R滑=$\frac{E}{{I}_{0}}$,
滑动变阻器与电阻丝总电阻:R+R滑=$\frac{E}{I}$,则电阻丝电阻:R=$\frac{E}{I}$-$\frac{E}{{I}_{0}}$.
④由图示螺旋测微器可知,其示数:d=0mm+20.0×0.01mm=0.200mm.
⑤根据图a所示电路,由欧姆定律可知:I=$\frac{E}{R+{R}_{滑}}$,$\frac{1}{I}$=$\frac{R}{E}$+$\frac{{R}_{滑}}{E}$=$\frac{ρ}{Eπ(\frac{d}{2})^{2}}$L+$\frac{{R}_{滑}}{E}$,
即:$\frac{1}{I}$=$\frac{ρ}{Eπ(\frac{d}{2})^{2}}$L+$\frac{{R}_{滑}}{E}$,$\frac{1}{I}$-L图象的斜率:k=$\frac{ρ}{Eπ(\frac{d}{2})^{2}}$,则电阻率:ρ=$\frac{kπE{d}^{2}}{4}$,
由图b所示图象可知,k=$\frac{4.0-2.0}{4000}$=0.0005A/m,把d、k代入ρ=$\frac{kπE{d}^{2}}{4}$解得:ρ≈6.3×10-7Ω/m;
故答案为:①C端;②$\frac{E}{I}$-$\frac{E}{{I}_{0}}$;④0.200;⑤$\frac{kπE{d}^{2}}{4}$;6.3×10-7.
点评 本题考查了实验注意事项、求电阻、螺旋测微器读数、求电阻率;螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器示数,读数时视线要与刻度线垂直,要注意可动刻度需要估读.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案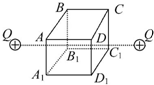 如图,真空中电量均为Q的两正点电荷,固定于一绝缘正方体框架的两侧面ABB1A1和DCC1D1中心连线上,且两电荷关于正方体中心对称,则( )
如图,真空中电量均为Q的两正点电荷,固定于一绝缘正方体框架的两侧面ABB1A1和DCC1D1中心连线上,且两电荷关于正方体中心对称,则( )| A. | A、B、C、D四个点的电势相同 | |
| B. | A1、B1、C1、D1四个点的电场强度相同 | |
| C. | 负检验电荷q在A点的电势能小于在C1点的电势能 | |
| D. | 正检验电荷q从C点移到C1点过程电场力对其做正功 |
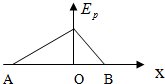 如图所示,空间存在着沿x轴方向的静电场,A、O、B为x轴上的点,图中的折线表示的是一带正电粒子沿x轴在A、B两点间运动时,其电势能EP随x的变化情况.若$\overline{AO}$>$\overline{OB}$,则下列判断正确的是( )
如图所示,空间存在着沿x轴方向的静电场,A、O、B为x轴上的点,图中的折线表示的是一带正电粒子沿x轴在A、B两点间运动时,其电势能EP随x的变化情况.若$\overline{AO}$>$\overline{OB}$,则下列判断正确的是( )| A. | A、B两点的电势一定相等 | |
| B. | 粒子从A向O运动过程中所受电场力均匀增大 | |
| C. | A、O间的电场强度大于O、B间的电场强度 | |
| D. | 若将一带负电的粒子从A点由静止释放,则当粒子运动到O点时动能最大 |
| A. | 从n=4的能级跃迁到低能级时,可能辐射出6种不同频率光子 | |
| B. | 从n=4的能级直接跃迁到n=1的能级,辐射出的光的波长最短 | |
| C. | 从n=4的能级跃迁到n=3的能级时,辐射出的光的频率最高 | |
| D. | 从n=4的能级跃迁到n=2的能级,辐射出的光子的能量最大 |
 在静电场中,一个电子只在电场力的作用下,沿着圆弧由A点运动到B点,在这个运动过程中,下列说法过程中正确的是( )
在静电场中,一个电子只在电场力的作用下,沿着圆弧由A点运动到B点,在这个运动过程中,下列说法过程中正确的是( )| A. | 该电子速度大小一定增加 | B. | A点的场强一定比B点的场强大 | ||
| C. | A、B两点的电势一定相等 | D. | 电子的电势能可能增大 |
 一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )
一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )| A. | E1<$\frac{kQ}{4{R}^{2}}$ | |
| B. | E2=$\frac{kQ}{4{R}^{2}}$ | |
| C. | 电荷Q在球心O处产生的场强方向垂直于底面向下 | |
| D. | 电荷Q在球心O处产生的场强方向垂直于底面向上 |
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 理想气体绝热压缩内能会增大 | |
| C. | 理想气体等温膨胀内能会减小 | |
| D. | 热量不可以从低温物体传到高温物体 |
 如图所示的是大型露天游乐场中的过山车,把过山车从很高的轨道一侧的顶端释放,它就不断地加速向下运动,最后冲上轨道另一端.你能用机械能守恒定律说明过山车为什么要从很高的轨道顶端释放吗?若环形轨道的半径为R,你认为过山车至少要从多高的轨道顶端释放?
如图所示的是大型露天游乐场中的过山车,把过山车从很高的轨道一侧的顶端释放,它就不断地加速向下运动,最后冲上轨道另一端.你能用机械能守恒定律说明过山车为什么要从很高的轨道顶端释放吗?若环形轨道的半径为R,你认为过山车至少要从多高的轨道顶端释放? 如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求:
如图所示,水平传送带的速度为4.0m/s,它的右端与等高的光滑水平平台相接触.将一质量为m=1kg的工件(可看成质点)轻轻放在传送带的左端,工件与传送带间的动摩擦因数μ=0.3,经过一段时间工件从光滑水平平台上滑出,恰好落在静止在平台下的小车的左端,小车的质量为M=2kg,小车与地面的摩擦可忽略.已知平台与小车的高度差h=0.8m,小车左端距平台右端的水平距离为s=1.2m,取g=10m/s2,求: