题目内容
8. 一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )
一半径为R的半球面均匀带有负电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{KQ}{2{R}^{2}}$.把半球面分为表面积相等的左、右两部分,如图所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E1、E2.则( )| A. | E1<$\frac{kQ}{4{R}^{2}}$ | |
| B. | E2=$\frac{kQ}{4{R}^{2}}$ | |
| C. | 电荷Q在球心O处产生的场强方向垂直于底面向下 | |
| D. | 电荷Q在球心O处产生的场强方向垂直于底面向上 |
分析 根据电场的叠加原理,分析半球壳在O点的场强方向,再比较场强的大小关系.根据E=k$\frac{Q}{{r}^{2}}$,结合左右两侧球壳上点电荷到O点距离的关系,进行分析.
解答 解:半球面分为表面积相等的左、右两部分,由于左右两个半个球壳在同一点产生的场强大小相等;由对称性可各,电荷Q在球心处产生的场强方向垂直底面向上;
则根据电场的叠加可知:左侧部分在O点产生的场强与右侧电荷在O点产生的场强大小相等,即E1=E2 .由于方向不共线,由合成法则可知,E1=E2 >$\frac{kQ}{4{R}^{2}}$;故ABC错误;D正确
故选:D.
点评 考查点电荷的电场强度的应用,知道电荷的分布,掌握矢量的叠加法则,对于此题采用“反证法”来区别选项的正误是很巧妙的,注意总结应用.

练习册系列答案
相关题目
9. 如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )
如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )
 如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )
如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )| A. | 恒为 $\frac{{nS({B_2}-{B_1})}}{{{t_2}-{t_1}}}$ | B. | 从0均匀变化到$\frac{{nS({B_2}-{B_1})}}{{{t_2}-{t_1}}}$ | ||
| C. | 恒为$-\frac{{nS({B_2}-{B_1})}}{{{t_2}-{t_1}}}$ | D. | 从0均匀变化到$-\frac{{nS({B_2}-{B_1})}}{{{t_2}-{t_1}}}$ |
3. 如图是安装在列车车厢之间的摩擦缓冲器结构的俯视图,图中①和②为楔块,楔块的斜面与水平的夹角为θ;③和④为垫板;弹簧a和弹簧b质量不计;楔块与弹簧盒、垫板之间均有摩擦,在车厢互相撞击使垫板③向盒里压进的过程中( )
如图是安装在列车车厢之间的摩擦缓冲器结构的俯视图,图中①和②为楔块,楔块的斜面与水平的夹角为θ;③和④为垫板;弹簧a和弹簧b质量不计;楔块与弹簧盒、垫板之间均有摩擦,在车厢互相撞击使垫板③向盒里压进的过程中( )
 如图是安装在列车车厢之间的摩擦缓冲器结构的俯视图,图中①和②为楔块,楔块的斜面与水平的夹角为θ;③和④为垫板;弹簧a和弹簧b质量不计;楔块与弹簧盒、垫板之间均有摩擦,在车厢互相撞击使垫板③向盒里压进的过程中( )
如图是安装在列车车厢之间的摩擦缓冲器结构的俯视图,图中①和②为楔块,楔块的斜面与水平的夹角为θ;③和④为垫板;弹簧a和弹簧b质量不计;楔块与弹簧盒、垫板之间均有摩擦,在车厢互相撞击使垫板③向盒里压进的过程中( )| A. | 弹簧a与弹簧b的压缩量之比是cotθ | |
| B. | 弹簧a与弹簧b的压缩量之比是2tanθ | |
| C. | 当弹簧压缩到最短的时候,楔块①的速度一定为零 | |
| D. | 当弹簧压缩到最短的时候,垫板③的速度一定为零 |
13.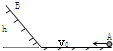 如图所示,小球以初速度v0从A点沿不光滑的轨道运动到高为h的B点后自动返回,其返回途中仍经过A点,水平轨道与倾斜轨道之间用平滑圆弧连接(图中没画出).则经过A点的速度大小为( )
如图所示,小球以初速度v0从A点沿不光滑的轨道运动到高为h的B点后自动返回,其返回途中仍经过A点,水平轨道与倾斜轨道之间用平滑圆弧连接(图中没画出).则经过A点的速度大小为( )
 如图所示,小球以初速度v0从A点沿不光滑的轨道运动到高为h的B点后自动返回,其返回途中仍经过A点,水平轨道与倾斜轨道之间用平滑圆弧连接(图中没画出).则经过A点的速度大小为( )
如图所示,小球以初速度v0从A点沿不光滑的轨道运动到高为h的B点后自动返回,其返回途中仍经过A点,水平轨道与倾斜轨道之间用平滑圆弧连接(图中没画出).则经过A点的速度大小为( )| A. | $\sqrt{{v}_{0}^{2}-4gh}$ | B. | $\sqrt{4gh-{v}_{0}^{2}}$ | C. | $\sqrt{{v}_{0}^{2}-2gh}$ | D. | v0 |
18.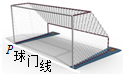 如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
 如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
如图所示为足球球门,球门宽为L,一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点),球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )| A. | 足球位移的大小x=$\sqrt{\frac{{L}^{2}}{4}+{s}^{2}}$ | |
| B. | 足球初速度的大小v0=$\sqrt{\frac{g}{2h}(\frac{{L}^{2}}{4}+{s}^{2})}$ | |
| C. | 足球末速度的大小v=$\sqrt{\frac{g}{2h}(\frac{{L}^{2}}{4}+{s}^{2})+4gh}$ | |
| D. | 足球初速度的方向与球门线夹角的正切值tanθ=$\frac{L}{2s}$ |

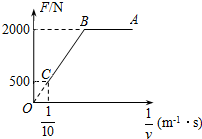 2013年5月18日第九届中国(北京)国际园林博览会开幕,为了方便游客游览,园中引进了无尾气无噪音的电动观光车,某辆电动观光车从静止开始沿平直公路行驶,达到的最大速度为36km/h,在此过程中,电动观光车发动机的牵引力F与对应速度的倒数$\frac{1}{v}$的关系图象如图所示(图中AB、BO均为直线),已知电动观光车的质量为1.2×103kg,行驶中所受的阻力恒定,则该车发动机的额定功率为5000W,从静止开始到发动机的功率达到额定功率所需要的时间为2s.
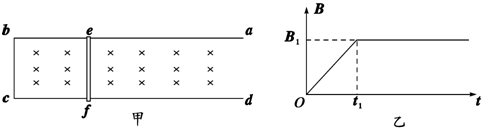
2013年5月18日第九届中国(北京)国际园林博览会开幕,为了方便游客游览,园中引进了无尾气无噪音的电动观光车,某辆电动观光车从静止开始沿平直公路行驶,达到的最大速度为36km/h,在此过程中,电动观光车发动机的牵引力F与对应速度的倒数$\frac{1}{v}$的关系图象如图所示(图中AB、BO均为直线),已知电动观光车的质量为1.2×103kg,行驶中所受的阻力恒定,则该车发动机的额定功率为5000W,从静止开始到发动机的功率达到额定功率所需要的时间为2s.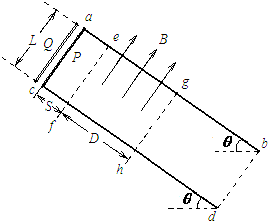 如图所示,电阻不计、间距L=1m、足够长的光滑金属导轨ab、cd与水平面成θ=37°角,导轨平面矩形区域efhg内分布着磁感应强度的大小B=1T,方向垂直导轨平面向上的匀强磁场,边界ef、gh之间的距离D=1.4m.现将质量m=0.1kg、电阻R=$\frac{5}{3}$Ω的导体棒P、Q相隔△t=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s.已知重力加速度g=10m/s2,sin37°=0.6,求
如图所示,电阻不计、间距L=1m、足够长的光滑金属导轨ab、cd与水平面成θ=37°角,导轨平面矩形区域efhg内分布着磁感应强度的大小B=1T,方向垂直导轨平面向上的匀强磁场,边界ef、gh之间的距离D=1.4m.现将质量m=0.1kg、电阻R=$\frac{5}{3}$Ω的导体棒P、Q相隔△t=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s.已知重力加速度g=10m/s2,sin37°=0.6,求