题目内容
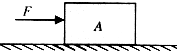
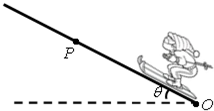
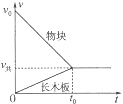
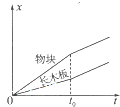
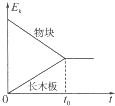
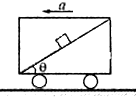
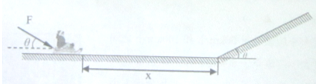
质量为30kg的小孩坐在质量为10kg的雪橇上,雪橇静止在地面上,离雪橇前端x=7m处有一个倾角θ=37°的斜坡,有一同伴在雪橇的后方施加F=200N的斜向下推力作用,推力F与水平方向的夹角为θ=37°,推力作用4s后撤去,已知雪橇与地面、雪橇与斜坡之间的动摩擦因数μ都是0.25,(小孩和雪橇可看成质点,若雪橇能冲上斜面,则不考虑从地面到斜坡的速度损失,sin37°=0.6,cos37°=0.8),问:
(1)撤去推力时,雪橇的速度多大?
(2)雪橇能否冲上斜面?如果能,请求出雪橇沿斜坡上升的最大距离,如果不能,请说明理由.
(1)撤去推力时,雪橇的速度多大?
(2)雪橇能否冲上斜面?如果能,请求出雪橇沿斜坡上升的最大距离,如果不能,请说明理由.

(1)根据牛顿第二定律得,雪橇的加速度a1=
=
=0.75m/s2,
则雪橇的速度v1=a1t1=0.75×4m/s=3m/s.
(2)雪橇匀加速直线运动的位移x1=
a1t12=
×0.75×16m=6m,
撤去拉力后在水平面上的加速度a2=
=-μg=-2.5m/s2,
根据v22-v12=2a(x-x1)
解得v2=2m/s.
此时仍可以冲上斜面,在斜面上的加速度a3=
=10×0.6+0.25×10×0.8=8m/s2.
沿斜面上滑的距离x3=
=
m=0.25m.
答:(1)撤去推力时,雪橇的速度是3m/s;
(2)雪橇能冲上斜面,雪橇沿斜坡上升的最大距离为0.25m.
| Fcos37°-μ(mg+Fsin37°) |
| m |
| 200×0.8-0.25×(400+200×0.6) |
| 40 |
则雪橇的速度v1=a1t1=0.75×4m/s=3m/s.
(2)雪橇匀加速直线运动的位移x1=
| 1 |
| 2 |
| 1 |
| 2 |
撤去拉力后在水平面上的加速度a2=
| -μmg |
| m |
根据v22-v12=2a(x-x1)
解得v2=2m/s.
此时仍可以冲上斜面,在斜面上的加速度a3=
| mgsin37°+μmgcos37° |
| m |
沿斜面上滑的距离x3=
| v22 |
| 2a3 |
| 4 |
| 16 |
答:(1)撤去推力时,雪橇的速度是3m/s;
(2)雪橇能冲上斜面,雪橇沿斜坡上升的最大距离为0.25m.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目