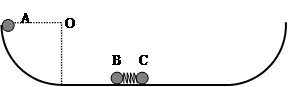题目内容
(12分) 如图甲所示，场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域，O点为该圆形区域的圆心，A点是圆形区域的最低点，B点是圆形区域最右侧的点。在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷，电荷的质量均为m，电量均为q，不计重力。试求：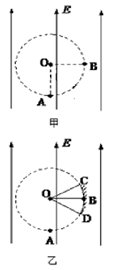
（1）运动轨迹经过B点的电荷在A点时的速度多大？
（2）若在圆形区域的边缘有一圆弧形接收屏CBD，B点仍是圆形区域最右侧的点，C、D分别为接收屏上最边缘的两点，如图乙所示，∠COB=∠BOD=37°。求该屏上接收到的电荷的末动能大小的范围。( 提示：sin37°=0.6，cos37°=0.8。)
（1）
；（2）
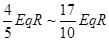
解析试题分析：（1）电荷在电场中只受电场力作用，由牛顿第二定律可知：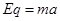
电荷在电场中做类平抛运动，设其在A点的速度为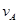
，则：
水平方向有：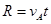
竖直方向有：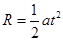
联立可解得：
（2）设圆周上任意点P与OA成θ角，如下图所示，电荷以初速度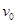
由A运动到P时间为t0，则：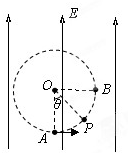
水平方向有：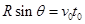
竖直方向有：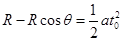
电荷在A点的动能：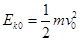
对电荷由A运动到P点使用动能定理有：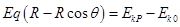
联立可解得：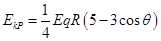
由此可知，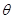
角增大，动能增大，故可知D点接收到的电荷的末动能最小，C点接收到的电荷的末动能最大；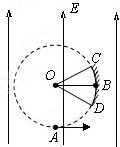
最小动能为：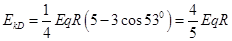
最大动能为：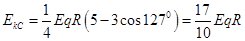
考点：运动的合成分解、带电粒子在电场中的运动、动能定理
练习册系列答案
应用题作业本系列答案
相关题目
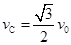，从此刻起在AB区域内加上一个水平向左的匀强电场，电场强度E保持不变，并且AB区域外始终不存在电场．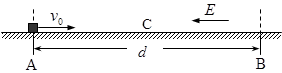
、
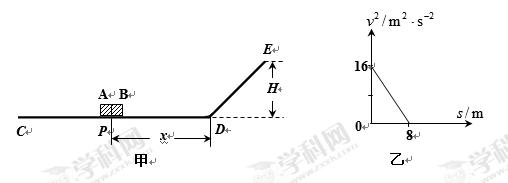
的小滑块A、B和一根轻质短弹簧，弹簧的一端与小滑块A粘连，另一端与小滑块B接触而不粘连.现使小滑块A和B之间夹着被压缩的轻质弹簧，处于锁定状态，一起以速度
在水平面上做匀速直线运动，如题8图所示.一段时间后，突然解除锁定（解除锁定没有机械能损失），两滑块仍沿水平面做直线运动，两滑块在水平面分离后，小滑块B冲上斜面的高度为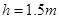
.斜面倾角
，小滑块与斜面间的动摩擦因数为
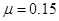，水平面与斜面圆滑连接.重力加速度
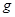取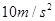
.求：（提示：
，
）
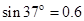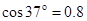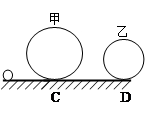
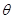=53O，具有动力装置的玩具小车质量为m=1kg，从A点开始以恒定功率P=10w由静止开始启动，运动至B点时撤去动力，小车继续沿圆弧轨道运动并冲出轨道。已知小车运动到B点时轨道对小车的支持力为FB=26
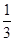N，小车在轨道AB上运动过程所受阻力大小恒为f=0.1mg小车可以被看成质点。取g=10m／s2，，sin53o=0.8，cos53o=0.6，求：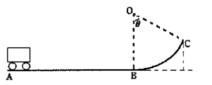
；
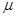圆弧轨道的最低点C相切，已知圆弧的半径为R，现把质量为m、带电荷量为＋Q的小球(可视为质点)由圆弧的最高点M静止释放，到最低点C时速度为v0.已知静电力常量为k，现取D为电势零点，求：
．一质量也为m的小球A从左侧的最高点自由滑下，A滑到水平面与B碰后立即粘在一起结合成D就不再分离（碰撞时间极短）．当D、C一起刚要滑到右侧最低点时，弹簧锁定解除且立即将C弹出并与弹簧分离．求
