题目内容
 过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:(1)物块经过第一轨道最高点时的速度大小;
(2)物块经过第二轨道最低点B时对轨道的压力大小;
(3)物块能够通过几个圆轨道?
分析:(1)物块在第一轨道运动的过程中机械能守恒,根据机械能守恒定律求出物块经过第一轨道最高点的速度大小.
(2)对A到B运用动能定理,求出到达B点时的速度,在B点重力和支持力的合力提供圆周运动的向心力,根据牛顿第二定律求出支持力的大小,从而求出物体对轨道的压力大小.
(3)设物块能够通过n个圆轨道,对全过程运用动能定理,求出第n个轨道的半径,抓住小球经过第n个圆轨道时,在最高点有临界值,即vn=
,运用数学知识求出n的范围.
(2)对A到B运用动能定理,求出到达B点时的速度,在B点重力和支持力的合力提供圆周运动的向心力,根据牛顿第二定律求出支持力的大小,从而求出物体对轨道的压力大小.
(3)设物块能够通过n个圆轨道,对全过程运用动能定理,求出第n个轨道的半径,抓住小球经过第n个圆轨道时,在最高点有临界值,即vn=
| gRn |
解答:解:(1)设经第一个轨道最高点的速度为v,由机械能守恒有
m
=
mv2+2mgR1
即有v=
=
=8m/s
故物块经过第一轨道最高点时的速度大小为8m/s.
(2)设物块经B点时的速度为vB,从A到B的过程由动能定理,
-μmg(R1+R2)=
m
-
m
对物块经B点受力分析,由向心力公式有
FN-mg=m
联立两式解得N=mg+m
=10+1×
=77.5N
由牛顿第三定律可知,物块对轨道的压力大小为77.5N.
故物块经过第二轨道最低点B时对轨道的压力大小为77.5N.
(3)设物块恰能通过第n个轨道,它通过第n个轨道的最高点时的速度为vn,有m
≥mg
对物块从A到第n个轨道的最高点的全过程由动能定理得-μmg[(R1+R2)+(R2+R3)+…(Rn-1+Rn)]-2mgRn=
m
-
m
又因为 Rn=kn-1R1=0.8n-1R1
由以上三式可整理得v02-2μg[(R1+R2+…+Rn-1)+(R2+R3+…+Rn)]≥5gRn
即
-2μg[
+
]=
-2μgR1
≥5gkn-1R1
将v0=12m/s,μ=0.5,R1=2m,k=0.8,g=10m/s2代入上式,整理得0.8n-1≥0.45,
即有(n-1)≤
≈3.6,解得 n≤4.6
故物块共可以通过4个圆轨道.
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
即有v=
|
| 122-4×10×2 |
故物块经过第一轨道最高点时的速度大小为8m/s.
(2)设物块经B点时的速度为vB,从A到B的过程由动能定理,
-μmg(R1+R2)=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 0 |
对物块经B点受力分析,由向心力公式有
FN-mg=m
| ||
| R2 |
联立两式解得N=mg+m
| ||
| R2 |
| 122-2×0.5×10×(2+1.6) |
| 1.6 |
由牛顿第三定律可知,物块对轨道的压力大小为77.5N.
故物块经过第二轨道最低点B时对轨道的压力大小为77.5N.
(3)设物块恰能通过第n个轨道,它通过第n个轨道的最高点时的速度为vn,有m
| ||
| Rn |
对物块从A到第n个轨道的最高点的全过程由动能定理得-μmg[(R1+R2)+(R2+R3)+…(Rn-1+Rn)]-2mgRn=
| 1 |
| 2 |
| v | 2 n |
| 1 |
| 2 |
| v | 2 0 |
又因为 Rn=kn-1R1=0.8n-1R1
由以上三式可整理得v02-2μg[(R1+R2+…+Rn-1)+(R2+R3+…+Rn)]≥5gRn
即
| v | 2 0 |
| R1(1-kn-1) |
| 1-k |
| R2(1-kn-1) |
| 1-k |
| v | 2 0 |
| (1+k)(1-kn-1) |
| 1-k |
将v0=12m/s,μ=0.5,R1=2m,k=0.8,g=10m/s2代入上式,整理得0.8n-1≥0.45,
即有(n-1)≤
| lg0.45 |
| lg0.8 |
故物块共可以通过4个圆轨道.
点评:本题综合运用了动能定理和机械能守恒定律,运用动能定理和机械能守恒定律解题注意要合理地选择研究的过程,列表达式求解.本题第(3)问较难,对数学的要求较高.

练习册系列答案
相关题目

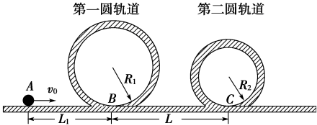 是一种过山车的简易模型,它由水平轨道和在竖直平面内的两个圆形轨道组成,C、D分别是两个圆形轨道的最低点,A、C间距与C、D问距相等,半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以
是一种过山车的简易模型,它由水平轨道和在竖直平面内的两个圆形轨道组成,C、D分别是两个圆形轨道的最低点,A、C间距与C、D问距相等,半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以
 过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求:
过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求: