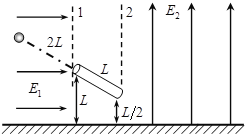Question

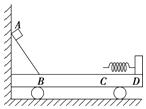
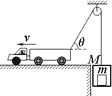
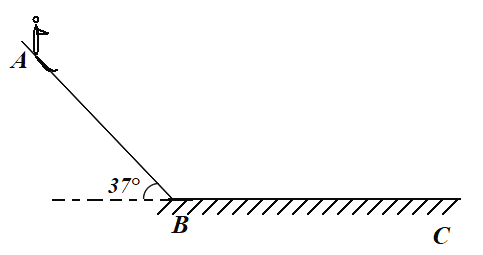
【题目】如图所示，甲坐在滑板上从距地面高为h＝2.4m的斜坡处A点由静止开始滑下，然后沿水平的滑道再滑行。同时乙从斜坡与水平滑道的交接处B点以某一速度v向右匀速直线运运动(图中未画出)，若滑板与斜坡滑道的动摩擦因数均为1＝0.5，滑板与水平滑道间的动摩擦因数为2＝，斜坡的倾角θ＝37°（sin37°＝0.6，cos37°＝0.8），斜坡与水平滑道间是平滑连接的，整个运动过程中空气阻力忽略不计，重力加速度g取10m/s2。求：

(1)人从斜坡上滑下时加速度为多大；

(2)人到达斜坡底端B时的速度是多少；

(3)为了避免甲、乙相碰，乙的速度v至少是多少。

Answer 1

【答案】(1)；(2)；(3)0.8m/s

【解析】

(1)由牛顿第二定律有：

　①

解得

②

(2)到达B的速度

③

　④

所有

⑤

(3)甲在水平方向减速时的加速度大小a1

⑥

甲在斜面运动的时间

⑦

若甲减少到v时恰好与乙车相碰，设此甲车在水平面减速的时间为t2，则有

⑧

⑨

有

即

（5v－4）（v-20)=0

解得

v=0.8m/s；t2=1s

或

v=20m/s；t2=-5s(舍去）⑩

所以乙的速度至少为0.8m/s。