Question

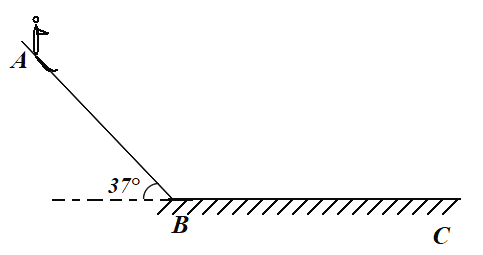
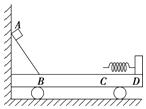
【题目】如图所示，光滑水平地面上停放着质量M=2kg的小车，小车上固定光滑斜面和连有轻弹簧的挡板，弹簧处于原长状态，其自由端恰在C点。质量m=1kg的小物块从斜面上A点由静止滑下并向右压缩弹簧。已知A点到B点的竖直高度差为h=1.8m，BC长度为L=3m，BC段动摩擦因数为0.3，CD段光滑，且小物块经B点时无能量损失。若取g=10m/s2，则下列说法正确的是（　　）

A.物块第一次到达C点时小车的速度为3m/s

B.弹簧压缩时弹性势能的最大值为3J

C.物块第二次到达C点时的速度为零

D.物块第二次到达C后物块与小车相对静止

Answer 1

【答案】BC

【解析】

A．物块从A下滑到B的过程中，根据动能定理得

解得

物块在BC段滑行时，物块和小车的系统动量守恒，以向右为正方向，根据动量守恒定律得

根据能量守恒定律得

联立解得

，

或

，（不合题意）

所以物块第一次到达C点时小车的速度为1m/s，故A错误；

B．当物块与小车的速度相等时弹簧压缩到最短，弹性势能最大，设物块与小车的共同速度为v，根据动量守恒定律

根据能量守恒定律得

解得弹簧压缩时弹性势能的最大值

故B正确；

CD．设物块第二次到达C点时的速度为，此时小车的速度为，根据动量守恒定律得

根据能量守恒定律，得

解得

，

或

，（不合题意）

所以物块第二次到达C点时的速度为零，第二次到达C后物块与小车没有相对静止，故D错误，C正确。

故选BC。