题目内容
【题目】如图所示，原长为L的轻质弹簧一端固定在O点，另一端与质量为，的圆环相连，圆环套在粗糙竖直固定杆上的A处，环与杆间动摩擦因数μ= 0.5，此时弹簧水平且处于原长。让圆环从A处由静止开始下滑，经过B处时速度最大，到达C处时速度为零。过程中弹簧始终在弹性限度之内。重力加速度为g。求
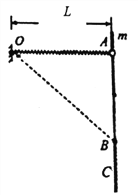
(1)圆环在A处的加速度为多大?
(2)若AB间距离为3L/4，则弹簧的劲度系数k为多少?
(3)若圆环到达C处时弹簧弹性势能为Ep，且AC =h，使圆环在C处时获得一个竖直向上的初速度，圆环恰好能到达A处。则这个初速度应为多大?
【答案】（1）
（2）
（3）
【解析】试题分析：（1）在A处只受重力做功，故根据牛顿第二定律可得
，解得
（2）圆环经过B处时，弹簧的弹力
设
，则
速度最大，合力为零，由平衡条件得：
联立解得
（3）圆环从A运动到C，由功能关系得
从C运动到A的过程，由功能关系得
又
解得
练习册系列答案
53随堂测系列答案
相关题目
