题目内容
【题目】如图所示,倾角 θ=37°的光滑且足够长的斜面固定在水平面上,在斜面顶端固定一个轮半径和质量不计的光滑定滑轮 D,质量均为m=1kg 的物体A和B用一劲度系数k=240N/m 的轻弹簧连接,物体 B 被位于斜面底端且垂直于斜面的挡板 P 挡住。用一不可伸长的轻绳使物体 A 跨过定滑轮与质量为 M 的小环 C 连接,小环 C 穿过竖直固定的光滑均匀细杆,当整个系统静止时,环 C 位 于 Q 处,绳与细杆的夹角 α=53°,且物体 B 对挡板 P 的压力恰好为零。图中 SD 水平且长度 为 d=0.2m,位置 R 与位置 Q 关于位置 S 对称,轻弹簧和定滑轮右侧的绳均与斜面平行。现 让环 C 从位置 R 由静止释放,sin37°=0.6,cos37°=0.8,g 取 10m/s2。
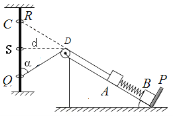
求:(1)小环 C 的质量 M;
(2)小环 C 通过位置 S 时的动能 Ek及环从位置 R 运动到位置 S 的过程中轻绳对环做的功 WT;
(3)小环 C 运动到位置 Q 的速率 v.
【答案】(1)0.72kg(2)0.3J(3)2m/s
【解析】(1)先以AB组成的整体为研究对象,AB系统受到重力.支持力和绳子的拉力处于平衡状态,则绳子的拉力为:T=2mgsinθ=2×10×sin37°=12N
以C为研究对象,则C受到重力、绳子的拉力和杆的弹力处于平衡状态,如图,则:Tcos53°=Mg
代入数据得:M=0.72kg
(2)由题意,开始时B恰好对挡板没有压力,所以B受到重力、支持力和弹簧的拉力,弹簧处于伸长状态;产生B沿斜面方向的受力:F1=mgsinθ=1×10×sin37°=6N
弹簧的伸长量:△x1=mgsinθ/K=0.025m
当小环 C 通过位置 S 时A下降的距离为xA=![]() =0.05m
=0.05m
此时弹簧的压缩量△x2=xA-△x1=0.025m
由速度分解可知此时A的速度为零,所以小环C从R运动到S的过程中,初末态的弹性势能相等,对于小环C、弹簧和A组成的系统机械能守恒有:Mgdcotα+mgxAsinθ=Ek
解得: Ek=1.38J
环从位置 R 运动到位置 S 的过程中,由动能定理可知: WT+ Mgdcotα= Ek
解得: WT=0.3J
⑶(5分)环从位置 R 运动到位置 Q 的过程中,对于小环C、弹簧和A组成的系统机械能守恒
Mg.(2dcotα)= ![]() vA =vcosα
vA =vcosα
两式联立可得: v=2m/s