题目内容
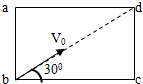如图所示的矩形区域abcd内有一个与此区域平面垂直的匀强磁场，已知矩形区域的边长是ab=L，bc=1.73L．一带电正粒子质量为m，电量为q，从b点沿与bc成30°角方向射入该磁场区域后，经时间t又从a点射出．现要加一平行与纸面的匀强电场，使上述粒子恰能从d点射出，不计重力，求磁场的方向和所加电场场强E的大小和方向．分析：（1）根据左手定则可以判断出磁场方向应垂直于纸面向里；
（2）根据牛顿第二定律，由洛伦兹力提供向心力，结合几何关系可确定半径的范围，即可求解磁场的强度和带电粒子的速度；加上一平行与纸面的匀强电场，粒子恰能从d点射出，说明了粒子受到的合力恰好为0，根据二力平衡即可求解．
（2）根据牛顿第二定律，由洛伦兹力提供向心力，结合几何关系可确定半径的范围，即可求解磁场的强度和带电粒子的速度；加上一平行与纸面的匀强电场，粒子恰能从d点射出，说明了粒子受到的合力恰好为0，根据二力平衡即可求解．
解答：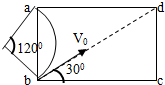
解：（1）如图，粒子从a点射出时，圆心角为120°，根据左手定则可以判断出磁场方向应垂直于纸面向里，
洛伦兹力提供圆周运动的向心力，得：qvB=
所以：r=
粒子运动的周期：T=
=
根据粒子运动的时间与周期的关系得：
=
联立以上各式得：B=
（2）由几何关系可得：r=
=
L
所以：v=
依题意，要使粒子恰能从d点射出，则粒子受到的电场力与洛伦兹力平衡，故电场方向应垂直于 bd向下且F洛=F电
即qvB=Eq
联立以上各式，整理得：E=vB═
答：磁场方向应垂直于纸面向里；电场方向应垂直于 bd向下，大小为E=
．
解：（1）如图，粒子从a点射出时，圆心角为120°，根据左手定则可以判断出磁场方向应垂直于纸面向里，洛伦兹力提供圆周运动的向心力，得：qvB=
| mv2 |
| r |
所以：r=
| mv |
| qB |
粒子运动的周期：T=
| 2πr |
| v |
| 2πm |
| qB |
根据粒子运动的时间与周期的关系得：
| t |
| T |
| θ |
| 360° |
联立以上各式得：B=
| 2πm |
| 3qt |
（2）由几何关系可得：r=
| ||
| cos30° |
| ||
| 3 |
所以：v=
2
| ||
| 9t |
依题意，要使粒子恰能从d点射出，则粒子受到的电场力与洛伦兹力平衡，故电场方向应垂直于 bd向下且F洛=F电
即qvB=Eq
联立以上各式，整理得：E=vB═
4
| ||
| 27qt2 |
答：磁场方向应垂直于纸面向里；电场方向应垂直于 bd向下，大小为E=
4
| ||
| 27qt2 |
点评：该题中的已知量比较少，要根据圆周运动的规律求解出粒子的速度和磁场的强度，然后再根据二力平衡的特点求出电场的强度和方向．属于中档题目．
练习册系列答案
阅读快车系列答案
相关题目
（2011?北京）利用电场和磁场，可以将比荷不同的离子分开，这种方法在化学分析和原子核技术等领域有重要的应用．如图所示的矩形区域ACDG（AC边足够长）中存在垂直于纸面的匀强磁场，A处有一狭缝．离子源产生的离子，经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场，运动到GA边，被相应的收集器收集．整个装置内部为真空．已知被加速的两种正离子的质量分别是m1和m2（m1＞m2），电荷量均为q．加速电场的电势差为U，离子进入电场时的初速度可以忽略．不计重力，也不考虑离子间的相互作用．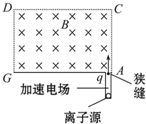
利用电场和磁场，可以将比荷不同的离子分开，这种方法在化学分析和原子核技术等领域有重要的应用．
和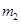
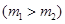，电荷量均为
.加速电场的电势差为
，离子进入电场时的初速度可以忽略.不计重力，也不考虑离子间的相互作用。
；
.