题目内容
 (2011?北京)利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭缝.离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场,运动到GA边,被相应的收集器收集.整个装置内部为真空.已知被加速的两种正离子的质量分别是m1和m2(m1>m2),电荷量均为q.加速电场的电势差为U,离子进入电场时的初速度可以忽略.不计重力,也不考虑离子间的相互作用.
(2011?北京)利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭缝.离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场,运动到GA边,被相应的收集器收集.整个装置内部为真空.已知被加速的两种正离子的质量分别是m1和m2(m1>m2),电荷量均为q.加速电场的电势差为U,离子进入电场时的初速度可以忽略.不计重力,也不考虑离子间的相互作用.(1)求质量为m1的离子进入磁场时的速率v1;
(2)当磁感应强度的大小为B时,求两种离子在GA边落点的间距s;
(3)在前面的讨论中忽略了狭缝宽度的影响,实际装置中狭缝具有一定宽度.若狭缝过宽,可能使两束离子在GA边上的落点区域交叠,导致两种离子无法完全分离.设磁感应强度大小可调,GA边长为定值L,狭缝宽度为d,狭缝右边缘在A处.离子可以从狭缝各处射入磁场,入射方向仍垂直于GA边且垂直于磁场.为保证上述两种离子能落在GA边上并被完全分离,求狭缝的最大宽度.
分析:(1)离子在电场中做加速运动,电场能转化为动能,由能量的转化和守恒即可求出离子进入磁场时的速度.
(2)离子在匀强磁场中将做匀速圆周运动,此时向心力提供洛伦兹力,由带电离子在磁场中运动的半径公式可分别求出质量为m1、m2的粒子的轨迹半径,两个轨迹的直径之差就是离子在GA边落点的间距.
(3)由题意画出草图,通过图找出两个轨迹因宽度为d狭缝的影响,从而应用几何知识找出各量的关系,列式求解.
(2)离子在匀强磁场中将做匀速圆周运动,此时向心力提供洛伦兹力,由带电离子在磁场中运动的半径公式可分别求出质量为m1、m2的粒子的轨迹半径,两个轨迹的直径之差就是离子在GA边落点的间距.
(3)由题意画出草图,通过图找出两个轨迹因宽度为d狭缝的影响,从而应用几何知识找出各量的关系,列式求解.
解答:解:
(1)动能定理 Uq=
m1
得:v1=
…①
(2)由牛顿第二定律和轨道半径有: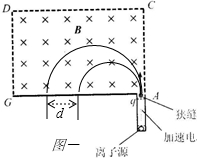
qvB=
,R=
利用①式得离子在磁场中的轨道半径为别为(如图一所示):
R1=
,R2=
…②
两种离子在GA上落点的间距s=2(R1-R2)=
(
-
)…③
(3)质量为m1的离子,在GA边上的落点都在其入射点左侧2R1处,由于狭缝的宽度为d,因此落点区域的宽度也是d(如图二中的细线所示).同理,质量为m2的离子在GA边上落点区域的宽度也是d(如图二中的粗线所示).为保证两种离子能完全分离,两个区域应无交叠,条件为2(R1-R2)>d…④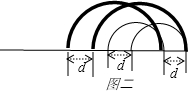
利用②式,代入④式得:2R1(1-
)>d
R1的最大值满足:
2R1m=L-d
得:(L-d)(1-
)>d
求得最大值:dm=
L.
(1)动能定理 Uq=
| 1 |
| 2 |
| v | 2 1 |
得:v1=
|
(2)由牛顿第二定律和轨道半径有:

qvB=
| mv2 |
| R |
| mv |
| qB |
利用①式得离子在磁场中的轨道半径为别为(如图一所示):
R1=
|
|
两种离子在GA上落点的间距s=2(R1-R2)=
|
| m1 |
| m2 |
(3)质量为m1的离子,在GA边上的落点都在其入射点左侧2R1处,由于狭缝的宽度为d,因此落点区域的宽度也是d(如图二中的细线所示).同理,质量为m2的离子在GA边上落点区域的宽度也是d(如图二中的粗线所示).为保证两种离子能完全分离,两个区域应无交叠,条件为2(R1-R2)>d…④

利用②式,代入④式得:2R1(1-
|
R1的最大值满足:
2R1m=L-d
得:(L-d)(1-
|
求得最大值:dm=
| ||||
2
|
点评:此题考查带电粒子在有界电场中运动的问题,类似质谱仪,解题方式和磁场中运动相似,确定圆心,轨迹和半径,整体上难度较低.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目