题目内容
 如图所示,电动机带着绷紧的传送皮带始终以υ0=2m/s的速度运动,传送带与水平面的夹角为300,现把一质量为 m=10kg的工件轻轻地放在皮带的底端,经过一段时间后,工件被送到高h=2m的平台上,己知工件与皮带间的动摩擦因数μ=
如图所示,电动机带着绷紧的传送皮带始终以υ0=2m/s的速度运动,传送带与水平面的夹角为300,现把一质量为 m=10kg的工件轻轻地放在皮带的底端,经过一段时间后,工件被送到高h=2m的平台上,己知工件与皮带间的动摩擦因数μ=| 3 |
分析:首先解出物体做匀加速运动的时间,以后物体做匀速直线运动;物体受到重力、支持力、和摩擦力的作用,合力沿斜面向上是物体加速运动,合力为零时物体匀速.由牛顿第二定律和运动学公式结合,分别求出物体与传送带相对运动过程中两个物体的位移,得到两者相对位移,由能量守恒求出电动机由于传送工件多消耗的电能.
解答:解:皮带的长度是L=
=4m.受力分析如图
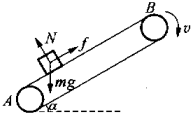 由牛顿第二定律有:μmgcosθ-mgsinθ=ma
由牛顿第二定律有:μmgcosθ-mgsinθ=ma
解得:a=2.5m/s2
设物体加速运动时间为t1,匀速运动时间为t2,由运动情况分析有:
物体匀加速运动的时间为 t1=
=
s=0.8s,位移为x1=
at2=0.8m<L,说明工件到达顶端前已与传送带相对静止.
则工件与传送带相对运动的位移为△x=v0t1-x1=0.8m
产生的热量为Q=μmgcos30°?△x=60J
根据能量守恒定律得
电动机由于传送工件多消耗的电能为 E=mgh+
m
+Q
代入解得,E=280J.
答:电动机由于传送工件多消耗的电能为280J.
| h |
| sin30° |
 由牛顿第二定律有:μmgcosθ-mgsinθ=ma
由牛顿第二定律有:μmgcosθ-mgsinθ=ma解得:a=2.5m/s2
设物体加速运动时间为t1,匀速运动时间为t2,由运动情况分析有:
物体匀加速运动的时间为 t1=
| v0 |
| a |
| 2 |
| 2.5 |
| 1 |
| 2 |
则工件与传送带相对运动的位移为△x=v0t1-x1=0.8m
产生的热量为Q=μmgcos30°?△x=60J
根据能量守恒定律得
电动机由于传送工件多消耗的电能为 E=mgh+
| 1 |
| 2 |
| v | 2 0 |
代入解得,E=280J.
答:电动机由于传送工件多消耗的电能为280J.
点评:本题一方面要分析工件的运动情况,由牛顿第二定律和运动学公式结合求解相对位移,即可求出摩擦产生的热量,另一方面要分析能量如何转化,由能量守恒定律求解电动机多消耗的电能.

练习册系列答案
相关题目
 (2010?烟台一模)如图所示,电动机带着绷紧的传送皮带始终以υ0=2m/s的速度运动,传送带与水平面的夹角为30°,现把某一工件轻轻地放在皮带的底端,经过一段时间后,工件被送到高h=2m的平台上,在此过程中电动机由于传送工件多消耗的电能为420J.已知工件与皮带间的动摩擦因数
(2010?烟台一模)如图所示,电动机带着绷紧的传送皮带始终以υ0=2m/s的速度运动,传送带与水平面的夹角为30°,现把某一工件轻轻地放在皮带的底端,经过一段时间后,工件被送到高h=2m的平台上,在此过程中电动机由于传送工件多消耗的电能为420J.已知工件与皮带间的动摩擦因数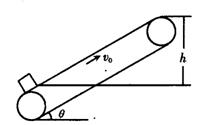
 =
= ,除此之外,不计其他损耗,则在皮带传送工件过程中产生的内能是多少?电动机增加消耗的电能是多少?
,除此之外,不计其他损耗,则在皮带传送工件过程中产生的内能是多少?电动机增加消耗的电能是多少?