题目内容
11.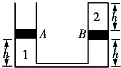 如图所示,系统由横截面积均为S 的两容器组成.左侧容器的侧壁可导热,足够高,上端开口.右侧容器的侧壁绝热,上端由导热材料封闭.两个容器的下端由可忽略容积的细管连通,两个绝热的活塞A、B下方封有理想气体1,B上方封有理想气体2.大气压强为p0,外界温度为T0,两活塞的重力均为0.5p0S.系统平衡时,两气体柱的高度如图所示.现将右侧容器上端和恒温热源连接,系统再次平衡时A上升了一定的高度.然后用外力将A 缓慢推回最初平衡时的位置并固定,系统第三次达到平衡后,理想气体2的长度变为1.2h.不计活塞与容器侧壁的摩擦,求:
如图所示,系统由横截面积均为S 的两容器组成.左侧容器的侧壁可导热,足够高,上端开口.右侧容器的侧壁绝热,上端由导热材料封闭.两个容器的下端由可忽略容积的细管连通,两个绝热的活塞A、B下方封有理想气体1,B上方封有理想气体2.大气压强为p0,外界温度为T0,两活塞的重力均为0.5p0S.系统平衡时,两气体柱的高度如图所示.现将右侧容器上端和恒温热源连接,系统再次平衡时A上升了一定的高度.然后用外力将A 缓慢推回最初平衡时的位置并固定,系统第三次达到平衡后,理想气体2的长度变为1.2h.不计活塞与容器侧壁的摩擦,求:①恒温热源的温度T;
②系统第二次平衡时活塞A 上升的高度△h.
分析 (1)对气体1由玻意耳定律可求得平衡后的压强;再对气体2由状态方程列式联立即可求得温度;
(2)对气体2由盖-吕萨克定律可求得后来的高度,则可求得高度的变化.
解答 解:①对气体1,初始时压强为1.5p0,和恒温热源相连后气体1 压强仍为1.5p0,体积不变,第三次平衡后压强为p1.
由玻意耳定律有1.5p0S×2h=p1S×1.8h
得p1=$\frac{5}{3}$P0
对气体2,初始时压强为p0,第二次平衡后压强不变,第三次平衡后压强为p1-0.5p0=$\frac{7{P}_{0}}{6}$
由理想气体的状态方程有:
$\frac{{P}_{0}sh}{{T}_{0}}$=$\frac{\frac{7}{6}{P}_{0}s×1.2h}{T}$
解得:T=1.4T0;
②对气体2,第二次平衡后气体柱高度为L,由盖-吕萨克定律有:
得L=1.4h
故第二次平衡时活塞A 上升的高度△h=L-h=0.4h
答:①恒温热源的温度T为1.4T0;
②系统第二次平衡时活塞A 上升的高度△h为0.4h
点评 本题主要考查气体实验定律,意在考查考生综合利用气体实验定律解决气体相关问题的能力;要注意要分别对两部分气体进行分析,选择合适的实验定律进行分析求解.

练习册系列答案
相关题目
1.在研究物体的运动时,下列物体中可以当做质点处理的是( )
| A. | 研究一端固定并可绕该端转动的木杆的运动时 | |
| B. | 研究用20cm长的细线拴着的一个直径为10cm的小球的摆动时 | |
| C. | 研究一体操运动员在平衡木上的运动时 | |
| D. | 研究月球绕地球运转时 |
2. 物理课上,老师做了一个奇妙的“跳环实验”.如图,她把一个带铁芯的线圈L、开关S和电源用导线连接起来后,将一铝质套环置于线圈L上,且使铁芯穿过套环.闭合开关S的瞬间,套环立刻跳起.
物理课上,老师做了一个奇妙的“跳环实验”.如图,她把一个带铁芯的线圈L、开关S和电源用导线连接起来后,将一铝质套环置于线圈L上,且使铁芯穿过套环.闭合开关S的瞬间,套环立刻跳起.
某同学另找来器材再探究此实验.他连接好电路,并将线圈上端与电源正极相连,经重复试验,置于线圈上的套环未动.对比老师演示的实验,下列四个选项中,导致套环未动的原因可能是( )
 物理课上,老师做了一个奇妙的“跳环实验”.如图,她把一个带铁芯的线圈L、开关S和电源用导线连接起来后,将一铝质套环置于线圈L上,且使铁芯穿过套环.闭合开关S的瞬间,套环立刻跳起.
物理课上,老师做了一个奇妙的“跳环实验”.如图,她把一个带铁芯的线圈L、开关S和电源用导线连接起来后,将一铝质套环置于线圈L上,且使铁芯穿过套环.闭合开关S的瞬间,套环立刻跳起.某同学另找来器材再探究此实验.他连接好电路,并将线圈上端与电源正极相连,经重复试验,置于线圈上的套环未动.对比老师演示的实验,下列四个选项中,导致套环未动的原因可能是( )
| A. | 线圈接在了直流电源上 | B. | 线圈与电源的正、负极接反了 | ||
| C. | 所选线圈的匝数过多 | D. | 所用套环的材料与老师的不同 |
6.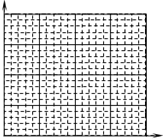 在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m数据如表:
在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m数据如表:
根据表数据,为直观反映F不变时a与m的关系,请在图2方格坐标纸中选择恰当物理量建立坐标系,并作出图线.
 在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m数据如表:
在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m数据如表:| 次 数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 小车加速度a/m•s-2 | 1.98 | 1.72 | 1.48 | 1.25 | 1.00 | 0.75 | 0.48 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 0.75 | 1.00 | 1.67 |
| 小车质量的倒数1/m/kg-1 | 4 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.33 | 1.00 | 0.60 |
16.下列说法中正确的是( )
| A. | 物体甲自发传递热量给物体乙,说明甲物体的温度一定比乙物体的温度高 | |
| B. | 物体内能增加,一定是物体从外界吸收了热量 | |
| C. | 当温度升高时,每个分子的运动都加快 | |
| D. | 布朗运动反映了液体分子的无规则运动 |
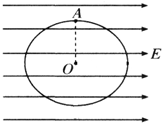 如图所示,一个竖直放置的半径为R的光滑绝缘环,置于水平方向的匀强电场中,电场强度为E.有一质量为m、电荷量为q的带正电的小球刚好能在环内侧做完整的圆周运动,并且小球所受静电力是其重力的$\frac{3}{4}$倍
如图所示,一个竖直放置的半径为R的光滑绝缘环,置于水平方向的匀强电场中,电场强度为E.有一质量为m、电荷量为q的带正电的小球刚好能在环内侧做完整的圆周运动,并且小球所受静电力是其重力的$\frac{3}{4}$倍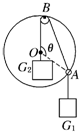 如图所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子不可伸长,求平衡时弦AB所对的圆心角θ.(可用三角函数表示,无受力分析图不得分)
如图所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子不可伸长,求平衡时弦AB所对的圆心角θ.(可用三角函数表示,无受力分析图不得分) 如图,一竖直放置的轻弹簧下端固定于桌面,现将一物块放于弹簧上同时对物块施加一竖直向下的外力,并使系统静止,若将外力突然撤去,则物块在第一次到达最高点前的速度-时间图象(图中实线)可能是图中的( )
如图,一竖直放置的轻弹簧下端固定于桌面,现将一物块放于弹簧上同时对物块施加一竖直向下的外力,并使系统静止,若将外力突然撤去,则物块在第一次到达最高点前的速度-时间图象(图中实线)可能是图中的( )



 如图所示,一个质量m=2kg的物体,受到与水平方向成37°角斜向上方的拉力F=10N,在水平地面上移动距离s=2m,物体与地面间的动摩擦因素μ=0.7,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,一个质量m=2kg的物体,受到与水平方向成37°角斜向上方的拉力F=10N,在水平地面上移动距离s=2m,物体与地面间的动摩擦因素μ=0.7,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: