题目内容
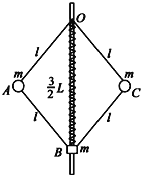
【题目】一转动装置如图所示，四根轻杆OA、OC、AB和CB与两小球以及一小环通过铰链连接，轻杆长均为l，球和环的质量均为m，O端固定在竖直的轻质转轴上，套在转轴上的轻质弹簧连接在O与小环之间，原长为L，装置静止时，弹簧长为
L，转动该装置并缓慢增大转速，小环缓慢上升．弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g，求：
（1）弹簧的劲度系数k；
（2）AB杆中弹力为零时，装置转动的角速度ω0
【答案】（1）
（2）
【解析】
试题分析：（1）装置静止时，设OA、AB杆中的弹力分别为F1、T1，OA杆与转轴的夹角为θ1．
小环受到弹簧的弹力F弹1＝k
，小环受力平衡：F弹1=mg+2T1cosθ1，
小球受力平衡：F1cosθ1+T1cosθ1-mg=0；F1sinθ1-T1sinθ1=0，
解得：
（2）设OA、AB杆中的弹力分别为F2、T2，OA杆与转轴的夹角为θ2，弹簧长度为x．
小环受到弹簧的弹力：F弹2=k（x-L）
小环受力平衡：F弹2=mg，
得：
对小球：F2cosθ2=mg；
F2sinθ2＝mω02lsinθ2；
解得：
【题目】某同学通过下述实验验证力的平行四边形定则。
实验步骤：
①将弹簧秤固定在贴有白纸的竖直木板上,使其轴线沿竖直方向。
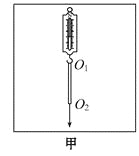
②如图甲所示,将环形橡皮筋一端挂在弹簧秤的秤钩上,另一端用圆珠笔尖竖直向下拉,直到弹簧秤示数为某一设定值时,将橡皮筋两端的位置标记为O1、O2,记录弹簧秤的示数F,测量并记录O1、O2间的距离（即橡皮筋的长度l）。每次将弹簧秤示数改变0．50 N,测出所对应的l,部分数据如下表所示：
F/N | 0 | 0．50 | 1．00 | 1．50 | 2．00 | 2．50 |
l/cm | l0 | 10．97 | 12．02 | 13．00 | 13．98 | 15．05 |
③找出②中F=2．50 N时橡皮筋两端的位置,重新标记为O、
,橡皮筋的拉力记为FOO′。
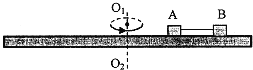
④在秤钩上涂抹少许润滑油,将橡皮筋搭在秤钩上,如图乙所示。用两圆珠笔尖成适当角度同时拉橡皮筋的两端,使秤钩的下端达到O点,将两笔尖的位置标记为A、B,橡皮筋OA段的拉力记为FOA,OB段的拉力记为FOB。
完成下列作图和填空：
（1）利用表中数据在给出的坐标纸上画出F-l图线。
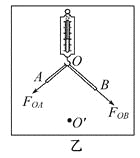
（2）测得OA=6．00cm,OB=7．60cm,则FOA的大小为 N。
（3）根据给出的标度,作出FOA和FOB的合力
的图示。
（4）通过比较与 的大小和方向,即可得出实验结论。