题目内容
【题目】(12分)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮(大小不计),滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A。半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响。现给滑块A施加一个水平向右、大小为60N的恒力F,求:
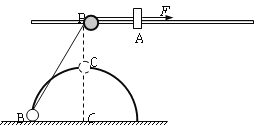
(1)把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功。
(2)小球B运动到C处时所受的向心力的大小。
(3)小球B被拉到离地多高时滑块A与小球B的速度大小相等?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)对于F的做功过程,有:,
,
所以,
(2)由于B球到达C处时,已无沿绳的分速度,所以此时滑块A的速度为零,
考察两球及绳子组成的系统的能量变化过程,由功能关系,得,
代入已知量,得,
因为向心力公式为,所以,代入已知量,得
(3)当绳与轨道相切时两球速度相等,由相似三角形知识,得
代入已知量,得,所以,

练习册系列答案
相关题目