题目内容
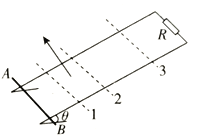
【题目】如图所示倾角为θ=30°的平行金属轨道固定在水平面上,导轨的顶端接有定值电阻R,长度与导轨宽度相等的导体棒AB垂直于导轨放置,,且保持与导轨由良好的接触.图中虚线1和2之间有垂直导轨平面向上的匀强磁场,现给导体棒沿导轨向上的初速度,使导体棒穿过磁场区域后能继续向上运动到最高位置虚线3,然后沿导轨向下运动到底端.已知导体棒向上运动经过虚线1和2时的速度大小之比为2:1,导体棒沿导轨向下运动由虚线2到1做匀速直线运动,虚线2、3之间的距离为虚线1、2之间距离的2倍,整个运动过程中导体棒所受的摩擦阻力恒为导体棒重力的![]() 除定值电阻外其余部分电阻均可忽略,求:
除定值电阻外其余部分电阻均可忽略,求:
(1)导体棒沿导轨1向上运动经过虚线2的速度v1与沿导轨向下运动经过虚线2的速度v2的比值;
(2)导体棒沿导轨向上运动经过磁场与沿导轨向下运动经过磁场的过程中,定值电阻R上产生的热量之比Q1:Q2为多大.
(3)导体棒沿导轨向上运动刚经过虚线1和刚到达虚线2时的加速度大小之比;
【答案】(1)![]() :1(2)10:1.(3)(2+2
:1(2)10:1.(3)(2+2![]() ):(2+
):(2+![]() )
)
【解析】(1)设虚线2、3之间的距离为x,导体棒由虚线2运动到虚线3的过程中,导体棒由虚线2运动到虚线3的过程中加速度大小为a1、导体棒由虚线3运动到虚线2的过程中加速度大小为a2,则由牛顿第二定律得:mgsin30°+![]() mg=ma1
mg=ma1
解得:a1=![]() g
g
由0-v12=2a1x,可得:v1=![]()
mgsin30°-![]() mg=ma2
mg=ma2
解得:a2=![]() g
g
由v22=2a2x,可得v2=![]()
因此v1:v2=![]() :1
:1
(2)(3)设导体棒的长度为L,导体棒沿导轨向上运动经过虚线1时的速度为v0,加速度大小为a3,则此时的感应电动势E1=BLv0
由闭合电路欧姆定律得,回路中的电流I1=![]()
此时导体棒所受安培力大小为F1=BI1L=![]() ,方向沿导轨向下
,方向沿导轨向下
由牛顿第二定律得:mgsin30°+![]() mg+F1=ma3
mg+F1=ma3
解得:a3=![]()
由题意可知导体棒由虚线3刚回到虚线2时速度大小为v2,此时的感应电动势为E2=BLv2
回路中的电流I2=![]()
此时导体棒所受安培力的大小为F2=BI2L=![]() ,方向沿导轨向上
,方向沿导轨向上
由力的平衡条件可得:mgsin30°=![]() mg+F2
mg+F2
解得:F2=![]() mg=
mg=![]()
又因为v1:v2=![]() :1,由题意知v0:v1=2:1,可得:v0:v2=2
:1,由题意知v0:v1=2:1,可得:v0:v2=2![]() :1
:1
整理可得:a3=![]() g
g
设导体棒刚好到达虚线2时的加速度为a4,根据牛顿第二定律则有:
mgsin30°+![]() mg+
mg+![]() =ma4
=ma4
整理可得:a4=![]() g
g
解得:a3:a4=(2+2![]() ):(2+
):(2+![]() )
)

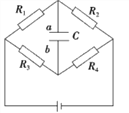
【题目】在测量电源的电动势和内阻的实验中,由于所用电压表(视为理想电压表)的量程较小,某同学设计了如图所示的实物电路.

(1)改变电阻箱的阻值R,分别测出阻值R0=10Ω的定值电阻两端的电压U.下列两组R的取值方案中,比较合理的方案是_________.(选填“1”或“2”)
方案编号 | 电阻箱的阻值R/Ω | ||||
1 | 400.0 | 350.0 | 300.0 | 250.0 | 200.0 |
2 | 80.0 | 70.0 | 60.0 | 50.0 | 40.0 |
(2)根据实验数据描点,以1/U为纵轴,R为横轴,绘出的1/U-R图象是一条直线.若直线的斜率为k,在1/U坐标轴上的截距为b,则该电源的电动势E=___,内阻r=___.(用k、b和R0表示)